Hiperbola

Za stilsku figuru, pogledajte Hiperbola (književnost)

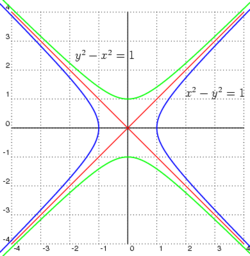
Hiperbola (starogrč. ύπερβολή, preterivanje) u matematici je algebarska kriva drugog reda u ravni, data sledećom jednačinom: ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$. Sastoji se iz dva simetrična dela, ima dva fokusa i dve asimptote date jednačinom $ay\pm bx=0$. Tačka preseka asimptota predstavlja centar simetrije hiperbole. Hiperbola, zajedno sa parabolom i elipsom, predstavlja tri tipa konusnih preseka. Konusni preseci se dobijaju u preseku ravni sa konusnom površinom (konusna površina se proteže u oba pravca).

Hiperbola je otvorena kriva sa dve grane, presek ravni sa obe polovine dvostrukog konusa.

Hiperbole x²-y²=1 i y²-x²=1

Hiperbola i njena 2 fokusa

Hiperbole nastaju na mnogo načina:

• kao kriva koja predstavlja funkciju i $y(x)=1/x$ u Dekartovoj ravni,
• kao staza koju prati senka vrha sunčanog sata,
• kao oblik otvorene orbite (za razliku od zatvorene eliptične orbite), kao što je orbita svemirske letelice tokom zamaha planete uz pomoć gravitacije ili, uopštenije, bilo koje svemirske letelice koja premašuje brzinu bekstva najbliže planete,
• kao putanja komete sa jednom pojavom (one koja putuje prebrzo da bi se ikada vratila u Sunčev sistem),
• kao putanja rasejanja subatomske čestice (na koju deluju odbojne umesto privlačne sile, ali princip je isti),
• u radio navigaciji, kada se može odrediti razlika između rastojanja do dve tačke, ali ne i same udaljenosti,

i tako dalje.

Svaka grana hiperbole ima dva kraka koji postaju ravniji (donja krivina) dalje od centra hiperbole. Dijagonalno suprotni krakovi, po jedan iz svake grane, teže u limitu ka zajedničkoj liniji, koja se naziva asimptota ta dva kraka. Dakle, postoje dve asimptote, čiji je presek u centru simetrije hiperbole, što se može smatrati tačkom ogledala oko koje se svaka grana odražava da bi formirala drugu granu. U slučaju krive $y(x)=1/x$ asimptote su dve koordinatne ose.

Hiperbole dele mnoga analitička svojstva elipse kao što su ekscentricitet, fokus i direktrisu. Obično se korespondencija može napraviti samo sa promenom predznaka u nekom terminu. Mnogi drugi matematički objekti imaju svoje poreklo u hiperboli, kao što su hiperbolički paraboloidi (površine sedla), hiperboloidi („korpe za otpatke“), hiperbolična geometrija (proslavljena neeuklidska geometrija Lobačevskog), hiperboličke funkcije (sinh, cosh, tanh, itd) , i žirovektorski prostori (geometrija predložena za upotrebu u relativističkoj i u kvantnoj mehanici koja nije Euklidska).

Etimologija i istorija

Reč „hiperbola“ potiče od grčke reči ὑπερβολή, što znači „premašeno“ ili „preterano“, od čega potiče i engleski izraz hyperbole. Hiperbole je otkrio Menehm u svojim istraživanjima problema udvostručavanja kocke, ali su tada nazvane preseci tupih konusa. Veruje se da je termin hiperbola skovao Apolonije iz Perge (oko 262–190. p. n. e.) u svom delu o konusnim presecima, Konikama. Nazivi druga dva opšta konusna preseka, elipsa i parabola, potiču od odgovarajućih grčkih reči za „nedostatak“ i „primenjen“; sva tri naziva su pozajmljena iz ranije pitagorejske terminologije koja se odnosila na poređenje stranice pravougaonika fiksne površine sa datim segmentom linije. Pravougaonik može da se „primeni“ na segment (što znači da ima jednaku dužinu), da bude kraći od segmenta ili da premaši segment.

Definicije

Kao lokus tačaka

Hiperbola: definicija rastojanjem tačaka do dve fiksne tačke (žarišta)

Hiperbola: definicija sa kružnom direktrisom

Hiperbola se može geometrijski definisati kao skup tačaka (lokus tačaka) u Euklidovoj ravni:

Hiperbola je skup tačaka, takav da je za bilo koju tačku skupa $P$ apsolutna razlika rastojanja $|PF_{1}|,\,|PF_{2}|$ na dve fiksne tačke $F_{1},F_{2}$ (žarišta) konstantna, obično se označava sa $2a,\,a>0:$

$H=\{P:||PF_{2}|-|PF_{1}||=2a\}\ .$

Srednja tačka segmenta linije $M$ koji spaja fokuse naziva se centar hiperbole. Linija koja prolazi kroz žarišta naziva se glavna osa. Ono sadrži vrhove $V_{1},V_{2}$, koji imaju rastojanje $a$ do centra. Udaljenost $c$ od fokusa do centra se naziva žižna udaljenost ili linearni ekscentricitet. Količnik ${\tfrac {c}{a}}$ je ekscentricitet $e$.

Jednačina $||PF_{2}|-|PF_{1}||=2a$ se može posmatrati na drugačiji način (pogledajte dijagram):
Ako je $c_{2}$ krug sa sredinom $F_{2}$ i poluprečnikom $2a$, tada je rastojanje tačke $P$ desne grane do kruga $c_{2}$ jednako rastojanju do fokusa $F_{1}$:

$|PF_{1}|=|Pc_{2}|.$

$c_{2}$ se naziva kružna direktrisa (povezana sa fokusom $F_{2}$) hiperbole. Da bi se dobila leva grana hiperbole, mora se koristiti kružna direktrisa srodna za $F_{1}$. Ovo svojstvo ne treba mešati sa definicijom hiperbole uz pomoć direktrise (linije) ispod.

Hiperbola sa jednačinom y = A/x

Rotiranje koordinatnog sistema da bi se pravougaona hiperbola opisala kao grafik funkcije

Tri pravougaone hiperbole $y=A/x$ sa koordinatnim osama kao asimptotama
crvena: A = 1; magenta: A = 4; plava: A = 9

Ako je 'xy-koordinatni sistem rotiran oko početka za ugao $-45^{\circ }$ i nove koordinate $\xi ,\eta$ su dodeljene, tada je $x={\tfrac {\xi +\eta }{\sqrt {2}}},\;y={\tfrac {-\xi +\eta }{\sqrt {2}}}$.
Pravougaona hiperbola ${\tfrac {x^{2}-y^{2}}{a^{2}}}=1$ (čije su poluose jednake) ima novu jednačinu ${\tfrac {2\xi \eta }{a^{2}}}=1$. Rešavanje za $\eta$ daje $\eta ={\tfrac {a^{2}/2}{\xi }}\ .$

Dakle, u sistemu xy-koordinata grafik funkcije $f:x\mapsto {\tfrac {A}{x}},\;A>0\;,$ sa jednačinom

$y={\frac {A}{x}}\;,A>0\;,$ je pravougaona hiperbola u potpunosti u prvom i trećem kvadrantu sa

• koordinatne ose kao asimptote,
• prava $y=x$ kao glavna osa,
• centar $(0,0)$ i polu-osa $a=b={\sqrt {2A}}\;,$
• vrhovi $\left({\sqrt {A}},{\sqrt {A}}\right),\left(-{\sqrt {A}},-{\sqrt {A}}\right)\;,$
• polu-konusni presek i poluprečnik zakrivljenosti na vrhovima $p=a={\sqrt {2A}}\;,$
• linearni ekscentricitet $c=2{\sqrt {A}}$ i ekscentricitet $e={\sqrt {2}}\;,$
• tangenta $y=-{\tfrac {A}{x_{0}^{2}}}x+2{\tfrac {A}{x_{0}}}$ u tački $(x_{0},A/x_{0})\;.$

Rotacija originalne hiperbole za $+45^{\circ }$ dovodi do pravougaone hiperbole u potpunosti u drugom i četvrtom kvadrantu, sa istim asimptotama, centar, konusni presek, poluprečnik zakrivljenosti na vrhovima, linearni ekscentricitet i ekscentricitet kao u slučaju rotacije $-45^{\circ }$, sa jednačinom

$y={\frac {-A}{x}}\;,A>0\;,$

• poluose $a=b={\sqrt {2A}}\;,$
• prava $y=-x$ kao glavna osa,
• temena $\left(-{\sqrt {A}},{\sqrt {A}}\right),\left({\sqrt {A}},-{\sqrt {A}}\right)\;.$

Pomeranje hiperbole sa jednačinom $y={\frac {A}{x}},\ A\neq 0\ ,$ tako da je novi centar $(c_{0},d_{0})$, daje novu jednačinu

$y={\frac {A}{x-c_{0}}}+d_{0}\;,$

a nove asimptote su $x=c_{0}$ i $y=d_{0}$.
Parametri oblika $a,b,p,c,e$ ostaju nepromenjeni.

Svojstva direktrise

Hiperbola: svojstvo direktrise

Hiperbola: definicija sa svojstvom direktrise

Dve prave na udaljenosti ${\textstyle d={\frac {a^{2}}{c}}}$ od centra i paralelno sa malom osom nazivaju se direktrise hiperbole (pogledajte dijagram).

Za proizvoljnu tačku $P$ hiperbole količnik udaljenosti do jednog fokusa i do odgovarajuće direktrise (pogledajte dijagram) je jednak ekscentricitetu:

${\frac {|PF_{1}|}{|Pl_{1}|}}={\frac {|PF_{2}|}{|Pl_{2}|}}=e={\frac {c}{a}}\ .$

Dokaz za par $F_{1},l_{1}$ sledi iz činjenice da $|PF_{1}|^{2}=(x-c)^{2}+y^{2},\ |Pl_{1}|^{2}=\left(x-{\tfrac {a^{2}}{c}}\right)^{2}$ i $y^{2}={\tfrac {b^{2}}{a^{2}}}x^{2}-b^{2}$ zadovoljavaju jednačinu

$|PF_{1}|^{2}-{\frac {c^{2}}{a^{2}}}|Pl_{1}|^{2}=0\ .$

Drugi slučaj se dokazuje analogno.

Prikaz konusa sa zajedničkim vrhom i zajedničkim polukonusnim presekom

Inverzna izjava je takođe tačna i može se koristiti za definisanje hiperbole (na način sličan definiciji parabole):

Za bilo koju tačku $F$ (fokus), bilo koja prava $l$ (direktrisa) nije kroz $F$ i bilo koji realni broj $e$ sa $e>1$ skup tačaka (lokus tačaka), za koji je količnik rastojanja do tačke i do prave je $e$

$H=\left\{P\,{\Biggr |}\,{\frac {|PF|}{|Pl|}}=e\right\}$

je hiperbola.

(Izbor $e=1$ daje parabolu i ako je $e<1$ elipsu.)

Dokaz

Neka je $F=(f,0),\ e>0$ i pretpostavimo da je $(0,0)$ tačka na krivoj. Direktrisa $l$ ima jednačinu $x=-{\tfrac {f}{e}}$. Sa $P=(x,y)$, relacija $|PF|^{2}=e^{2}|Pl|^{2}$ proizvodi jednačine

$(x-f)^{2}+y^{2}=e^{2}\left(x+{\tfrac {f}{e}}\right)^{2}=(ex+f)^{2}$ and $x^{2}(e^{2}-1)+2xf(1+e)-y^{2}=0.$

Zamena $p=f(1+e)$ daje

$x^{2}(e^{2}-1)+2px-y^{2}=0.$

Ovo je jednačina elipse ($e<1$) ili parabole ($e=1$) ili hiperbola ($e>1$). Svi ovi nedegenerisani konusi imaju zajedničko poreklo kao vrh (vidi dijagram).

Ako je $e>1$, uvedite nove parametre $a,b$ tako da je $e^{2}-1={\tfrac {b^{2}}{a^{2}}},{\text{ и }}\ p={\tfrac {b^{2}}{a}}$, a onda gornja jednačina postaje

${\tfrac {(x+a)^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1\ ,$

što je jednačina hiperbole sa centrom $(-a,0)$, x-osom kao glavnom osom i glavnom/sporednom poluosom $a,b$.

Jednačine hiperbole

Parametarska jednačine hiperbole je: ${\begin{cases}x=a\sec \alpha \\y=b\tan \alpha \end{cases}}$

U Dekartovom koordinatnom sistemu, hiperbola se opisuje jednačinom:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.$

Osobine

Postoje dve važne osobine fokusa hiperbole $F_{1},F_{2}$:

1. Za svaku tačku hiperbole R, važi (d je rastojanje): $\qquad \mid d(P,F_{1})-d(P,F_{2})\mid =2a\qquad a\in \mathbb {R}$
   Ovo svojstvo omogućava i sledeću definiciju hiperbole: Geometrijsko mesto tačaka u ravni, za koje je apsolutna vrednost razlike rastojanja od bilo koje tačke do dve fiksne tačke u istoj ravni (dva fokusa), konstantna.
2. Tangenta na svaku tačku hiperbole R predstavlja bisektrisu $\angle F_{1}PF_{2}$.

Dužina luka

Dužina luka hiperbole nema elementaran izraz. Gornja polovina hiperbole može se parametrizovati kao

$$y=b{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}.$$

Tada se integral koji daje dužinu luka $s$ od $x_{1}$ do $x_{2}$ može izračunati kao:

$$s=b\int _{\operatorname {arcosh} {\frac {x_{1}}{a}}}^{\operatorname {arcosh} {\frac {x_{2}}{a}}}{\sqrt {1+\left(1+{\frac {a^{2}}{b^{2}}}\right)\sinh ^{2}v}}\,\mathrm {d} v.$$

Nakon upotrebe zamene $z=iv$, ovo se takođe može predstaviti korišćenjem nepotpunog eliptičkog integrala druge vrste $E$ sa parametrom $m=k^{2}$:

$$s=ib{\Biggr [}E\left(iv\,{\Biggr |}\,1+{\frac {a^{2}}{b^{2}}}\right){\Biggr ]}_{\operatorname {arcosh} {\frac {x_{2}}{a}}}^{\operatorname {arcosh} {\frac {x_{1}}{a}}}.$$

Koristeći samo realne brojeve, ovo postaje

$$s=b\left[F\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)-E\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)+{\sqrt {1+{\frac {a^{2}}{b^{2}}}\tanh ^{2}v}}\,\sinh v\right]_{\operatorname {arcosh} {\tfrac {x_{1}}{a}}}^{\operatorname {arcosh} {\tfrac {x_{2}}{a}}}$$

gde je $F$ nepotpuni eliptički integral prve vrste sa parametrom $m=k^{2}$ i $\operatorname {gd} v=\arctan \sinh v$ je Gudermanova funkcija.

Literatura

• Kazarinoff, Nicholas D. (2003), Ruler and the Round, Mineola, N.Y.: Dover, ISBN 0-486-42515-0 
• Oakley, C. O., Ph.D. (1944), An Outline of the Calculus, New York: Barnes & Noble 
• Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd izd.), Reading: Addison-Wesley, LCCN 76087042 
• Woodhouse, N. M. J. (2003), Special Relativity, London: Springer, str. 71, ISBN 978-1-85233-426-0 
• Abramowitz, Milton; Stegun, Irene A., ur. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, ISBN 978-0-486-61272-0 
• Rickey, V. Frederick; Tuchinsky, Philip M. (1980). „An application of geography to mathematics: History of the integral of the secant” (PDF). Mathematics Magazine. 53 (3): 162—166. doi:10.1080/0025570X.1980.11976846. 
• Ringermacher, Harry I.; Mead, Lawrence R. (2009). „A new formula describing the scaffold structure of spiral galaxies”. Monthly Notices of the Royal Astronomical Society. 397 (1): 164—171. doi:10.1111/j.1365-2966.2009.14950.x . 
• Robertson, John S. (1997). „Gudermann and the simple pendulum”. The College Mathematics Journal. 28 (4): 271—276. JSTOR 2687148. doi:10.2307/2687148. 
• Romakina, Lyudmila N. (2018). „The inverse Gudermannian in the hyperbolic geometry”. Integral Transforms and Special Functions. 29 (5): 384—401. doi:10.1080/10652469.2018.1441296. 
• Roy, Ranjan; Olver, Frank W. J. (2010), „4. Elementary Functions”, Ur.: Olver, Frank W. J.; et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248 .
• Sala, Kenneth L. (1989). „Transformations of the Jacobian amplitude function and its calculation via the arithmetic-geometric mean” (PDF). SIAM Journal on Mathematical Analysis. 20 (6): 1514—1528. doi:10.1137/0520100. 

Spoljašnje veze

• Informacije o hiperboli
• Hazewinkel Michiel, ur. (2001). „Hyperbola”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
• Apollonius' Derivation of the Hyperbola at Convergence
• Frans van Schooten: Mathematische Oeffeningen, 1659
• Weisstein, Eric W. „Hiperbola”. MathWorld.