Пирамида (геометрија)
Пирамида (од грчки πυραμίς (pyramís)[1][2]) полиедар је омеђен основом и страницама које се спајају у једној тачки - темену, које се налази на супротној страни од основе. Пирамида може бити права или коса. Права пирамида је она код које се ортогонална пројекција темена (врха) на основу поклапа са тежиштем основе. Права пирамида је правилна ако јој је основа правилан многоугао.[3][4] Површина пирамиде једнака је збиру површина основе и страница. Основа може бити било који многоугао, док су странице заправо троуглови. Код правилне пирамиде ти троуглови су једнакокраки и међусобно подударни. Површина пирамиде се израчунава: , где је: B - површина основе, M - површина омотача. Запремина пирамиде се рачуна по формули: , где је: B - површина основе, H - висина пирамиде
| Праве пирамиде са регуларном основом | |
|---|---|
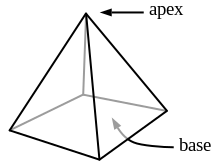 Пример: квадратна пирамида | |
| Стране | n троуглови 1 n-sided полигон |
| Ивице | 2n |
| Темена | n + 1 |
| Шлафлијев симбол | ( ) ∨ {n} |
| Конвејова нотација | Yn |
| Група симетрије | Cnv, [1,n], (*nn), реда 2n |
| Група ротације | Cn, [1,n]+, (nn), реда n |
| Дуални полиедар | самодуалан |
| Својства | конвексна |


Међу косим пирамидама, попут оних са оштрим и тупим троугловима, пирамида се може назвати оштром ако је њен врх изнад унутрашњости основе и тупом ако јој је врх изнад спољашњости основе. Правоугаона пирамида има врх изнад ивице или темена основе. У тетраедру ови квалификатори се мењају на основу тога које лице се сматра базом.
Пирамиде су класа призматоида. Пирамиде се могу удвостручити у бипирамиде додавањем друге тачке померања на другој страни основне равни.
Праве пирамиде са регуларном основом уреди
Права пирамида са регуларном основом има странице једнакокраког троугла, са симетријом Cnv или [1,n], и са редом 2n. Њој се може дати проширени Шлафли симбол ( ) ∨ {n}, који представља тачку, ( ), спојену (ортогонално померену) са регуларним полигоном, {n}. Операција спајања ствара нову ивицу између свих парова темена две спојене фигуре.[5]
Тригонална или троугласта пирамида са свим површинама једнакостраничног троугла постаје регуларни тетраедар, једно од Платонових чврстих тела. Случај ниже симетрије троугласте пирамиде је C3v, која има основу једнакостраничног троугла и 3 идентичне странице једнакокраког троугла. Квадратне и петоугаоне пирамиде такође могу бити састављене од правилних конвексних многоуглова, у ком случају су то Џонсонова тела.
Ако су све ивице квадратне пирамиде (или било ког конвексног полиедра) тангентне на сферу тако да је просечан положај тангенцијалних тачака у центру сфере, тада се каже да је пирамида канонска и чини половину правилног октаедра.
Пирамиде са шестоуглом или вишом основом морају бити састављене од једнакокраких троуглова. Шестоугаона пирамида са једнакостраничним троугловима била би потпуно равна фигура, а седмоугаона или виша би имала троуглове који се уопште не би састајали.
Права звездасте пирамиде уреди
Праве пирамиде са правилним звездастим полигонским базама називају се звездасте пирамиде.[6] На пример, пентаграмска пирамида има основу пентаграма и 10 троугластих страница које се секу.
Праве пирамиде са неправилном основом уреди
Права пирамида се може назвати као ( )∨P, где је ( ) тачка врха, ∨ оператор спајања, и P је основни полигон.
Једнакостранични троугао правог тетраедра може се написати као ( )∨[( )∨{ }] као спој тачке са основом једнакокраког троугла, као [( )∨( )]∨{ } или { }∨{ } као спој (ортогонални помаци) два ортогонална сегмента, дигонални дисфеноид, који садржи 4 лица једнакокраког троугла. Он има C1v симетрију из две различите оријентације базе и врха, а C2v у својој пуној симетрији.
Правоугаона права пирамида, написана као ( )∨[{ }×{ }], и ромбична пирамида, као ( )∨[{ }+{ }], обе имају симетрију C2v.
| Правоугаона пирамида | Ромбична пирамида |
|---|
Запремина уреди
Запремина пирамиде (такође било којег конуса) је , где је b површина основе, а h висина од основе до врха. Ово функционише за било који полигон, правилан или неправилан, и било коју локацију врха, под условом да се h мери као окомито растојање од равни која садржи основу. Године 499, Арјабхата, математичар-астроном из класичног доба индијске математике и индијске астрономије, користио је ову методу у Аријабатији (одељак 2.6).
Формула се може формално доказати помоћу калкулуса. По сличности, линеарне димензије попречног пресека паралелног основици расту линеарно од врха до основе. Фактор скалирања (фактор пропорционалности) је , или , где је h висина, а y окомито растојање од равни основе до попречног пресека. Пошто је површина било ког попречног пресека пропорционална квадрату фактора скалирања облика, површина попречног пресека на висини y је , или пошто су b и h константе, . Запремина је дата интегралом
Иста једначина, , важи и за конусе са било којим база. Ово се може доказати аргументом сличним оном изнад; погледајте запремину конуса.
На пример, запремина пирамиде чија је основа n-страни правилан многоугао са дужином странице s и чија је висина h је
Формула се такође може извести тачно без рачуна за пирамиде са правоугаоним основама. Замислите јединичну коцку. Нацртајте линије од центра коцке до сваког од 8 врхова. Ово дели коцку на 6 једнаких квадратних пирамида основне површине 1 и висине 1/2. Свака пирамида јасно има запремину од 1/6. Из овога се закључује да је запремина пирамиде = висина × површина основе / 3.
Затим се коцка може проширити у три правца за неједнаке количине тако да добијене правоугаоне чврсте ивице буду a, b и c, са чврстом запремином abc. Свака од 6 пирамида унутар ње је такође проширена. Свака пирамида има исту запремину abc/6. Пошто парови пирамида имају висине a/2, b/2 и c/2, види се да је запремина пирамиде = висина × површина основе / 3 поново.
Када су бочни троуглови једнакостранични, формула за запремину је
Ова формула важи само за n = 2, 3, 4 и 5; а такође покрива случај n = 6, за који је запремина једнака нули (тј. висина пирамиде је нула).
Површина уреди
Површина пирамиде је , где је B основна површина, P је основни периметар, а висина нагиба , где је h висина пирамиде, а r полупречник основе.
Центроид уреди
Центроид пирамиде налази се на сегменту праве који повезује врх са центроидом основе. За пирамиду, тежиште је 1/4 удаљености од основе до врха.
n-димензионалне пирамиде уреди
Дводимензионална пирамида је троугао, формиран од основне ивице повезане са неколинеарном тачком која се зове врх.
4-димензионална пирамида се назива полиедарска пирамида, конструисана од полиедра у 3-просторној хиперравни 4-простора са другом тачком изван те хиперравне.
Пирамиде виших димензија су слично конструисане.
Породица симпликса представља пирамиде у било којој димензији, растући од троугла, тетраедра, 5-ћелија, 5-симплекса, итд. n-димензионални симплекс има минимум n+1 врхова, са свим паровима врхова повезаних ивицама, све тројке врхова који дефинишу лица, све четворке тачака које дефинишу тетраедарске ћелије, итд.
Полиедарска пирамида уреди
У 4-димензионалној геометрији, полиедарска пирамида је 4-политоп конструисан од основне ћелије полиедра и тачке врха. Бочни фасети су пирамидалне ћелије, од којих је свака изграђена од једне стране основног полиедра и врха. Врхови и ивице полиедарских пирамида чине примере графова врхова, графова формираних додавањем једног темена (врха) на планарни граф (граф базе).
Регуларни 5-ћелијски (или 4-симплекс) је пример тетраедарске пирамиде. Униформни полиедри са полупречником круга мањим од 1 могу се правити полиедарске пирамиде са правилним тетраедарским страницама. Полиедар са v врховима, e ивицама и f површинама може бити основа на полиедарској пирамиди са v+1 врховима, e+v ивицама, f+e површинама и 1+f ћелијама.
4Д полиедарска пирамида са аксијалном симетријом може се визуализовати у 3Д помоћу Шлегеловог дијаграма — 3Д пројекције која поставља врх у центар основног полиедра.
| Симетрија | [1,1,4] | [1,2,3] | [1,3,3] | [1,4,3] | [1,5,3] | |
|---|---|---|---|---|---|---|
| Назив | Квадратно-пирамидална пирамида | Троугласто призматична пирамида | Тетраедарска пирамида | Кубна пирамида | Октаедарска пирамида | Икосаедарска пирамида |
| Сегментохорни индекс[7] |
K4.4 | K4.7 | K4.1 | K4.26.1 | K4.3 | K4.84 |
| Висина | 0,707107 | 0,645497 | 0,790569 | 0,500000 | 0,707107 | 0,309017 |
| Слика (Основа) |
||||||
| Основа | Квадратна пирамида |
Троугласта призма |
Тетраедар | Коцка | Октаедар | Икосаедар |
Сваки конвексни 4-политоп се може поделити на полиедарске пирамиде додавањем унутрашње тачке и стварањем једне пирамиде од сваког фасета до централне тачке. Ово може бити корисно за израчунавање волумена.
4-димензионална хиперзапремина полиедарске пирамиде је 1/4 запремине основног полиедра пута његова висина окомито, у поређењу са површином троугла која је 1/2 дужине основе пута висина, и запремина пирамиде да је 1/3 површине основе пута висина.
3-димензионална површинска запремина полиедарске пирамиде је , где је B основна запремина, A је површина основне површине, а Л висина нагиба (висина бочних пирамидалних ћелија) , где је h висина, а r полупречник.
Види још уреди
- Пирамиде (конструкције)
- Бипирамида
- Тригонална пирамида (хемија)
Референце уреди
- ^ πυραμίς, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus Digital Library
- ^ The word meant "a kind of cake of roasted wheat-grains preserved in honey"; the Egyptian pyramids were named after its form (R. S. P. Beekes, Etymological Dictionary of Greek, Brill, 2009, p. 1261).
- ^ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p. 46
- ^ Civil Engineers' Pocket Book: A Reference-book for Engineers Архивирано 2018-02-25 на сајту Wayback Machine
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, стр. 50, ISBN 978-0-521-09859-5, Архивирано из оригинала 2013-12-11. г..
- ^ Convex Segmentochora Архивирано 2014-04-19 на сајту Wayback Machine Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1–4, 139–181, 2000
Литература уреди
- Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. стр. xiv. ISBN 978-0-8160-4953-0.
- Vincenzo De Risi (2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Birkhäuser. стр. 1—. ISBN 978-3-319-12102-4.
- Walter A. Meyer (2006). Geometry and Its Applications. Elsevier. ISBN 978-0-08-047803-6.
- J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277–318.
- Neugebauer, Otto (1969) [1957]. „Chap. IV Egyptian Mathematics and Astronomy”. The Exact Sciences in Antiquity (2 изд.). Dover Publications. стр. 71—96. ISBN 978-0-486-22332-2.
- Ossendrijver, Mathieu (29. 1. 2016). „Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph”. Science. 351 (6272): 482—484. Bibcode:2016Sci...351..482O. PMID 26823423. S2CID 206644971. doi:10.1126/science.aad8085.
- Depuydt, Leo (1. 1. 1998). „Gnomons at Meroë and Early Trigonometry”. The Journal of Egyptian Archaeology. 84: 171—180. JSTOR 3822211. doi:10.2307/3822211.
- Slayman, Andrew (27. 5. 1998). „Neolithic Skywatchers”. Archaeology Magazine Archive. Архивирано из оригинала 5. 6. 2011. г. Приступљено 17. 4. 2011.
- Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.
- Kurt Von Fritz (1945). „The Discovery of Incommensurability by Hippasus of Metapontum”. The Annals of Mathematics.
- James R. Choike (1980). „The Pentagram and the Discovery of an Irrational Number”. The Two-Year College Mathematics Journal.
- Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0
- O'Connor, J.J.; Robertson, E.F. (фебруар 1996). „A history of calculus”. University of St Andrews. Архивирано из оригинала 15. 7. 2007. г. Приступљено 7. 8. 2007.
- Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2nd изд.), Reading: Addison-Wesley, LCCN 76087042

