Teorema četiri boje — разлика између измена

Садржај обрисан Садржај додат

Инлајн

Верзија на датум 18. фебруар 2020. у 09:51

U matematici, teorema četiri boje, ili teorema mape s četiri boje, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet.^[1] It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand.^[2] Since then the proof has gained wide acceptance, although some doubters remain.^[3]

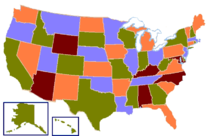
The four color theorem was proved in 1976 by Kenneth Appel and Wolfgang Haken after many false proofs and counterexamples (unlike the five color theorem, a theorem that states that five colors are enough to color a map, which was proved in the 1800s). To dispel any remaining doubts about the Appel–Haken proof, a simpler proof using the same ideas and still relying on computers was published in 1997 by Robertson, Sanders, Seymour, and Thomas. Additionally, in 2005, the theorem was proved by Georges Gonthier with general-purpose theorem-proving software.

Precizna formulacija teoreme

In graph-theoretic terms, the theorem states that for loopless planar $G$ , the chromatic number of its dual graph is $\chi (G^{*})\leq 4$ .

The intuitive statement of the four color theorem, i.e. "given any separation of a plane into contiguous regions, the regions can be colored using at most four colors so that no two adjacent regions have the same color", needs to be interpreted appropriately to be correct.

First, regions are adjacent if they share a boundary segment; two regions that share only isolated boundary points are not considered adjacent. Second, bizarre regions, such as those with finite area but infinitely long perimeter, are not allowed; maps with such regions can require more than four colors.^[4] (To be safe, we can restrict to regions whose boundaries consist of finitely many straight line segments. It is allowed that a region entirely surround one or more other regions.) Note that the notion of "contiguous region" (technically: connected open subset of the plane) is not the same as that of a "country" on regular maps, since countries need not be contiguous (e.g., the Cabinda Province as part of Angola, Nakhchivan as part of Azerbaijan, Kaliningrad as part of Russia, and Alaska as part of the United States are not contiguous). If we required the entire territory of a country to receive the same color, then four colors are not always sufficient. For instance, consider a simplified map:

In this map, the two regions labeled A belong to the same country. If we wanted those regions to receive the same color, then five colors would be required, since the two A regions together are adjacent to four other regions, each of which is adjacent to all the others. A similar construction also applies if a single color is used for all bodies of water, as is usual on real maps. For maps in which more than one country may have multiple disconnected regions, six or more colors might be required.

A map with four regions, and the corresponding planar graph with four vertices.

A simpler statement of the theorem uses graph theory. The set of regions of a map can be represented more abstractly as an undirected graph that has a vertex for each region and an edge for every pair of regions that share a boundary segment. This graph is planar: it can be drawn in the plane without crossings by placing each vertex at an arbitrarily chosen location within the region to which it corresponds, and by drawing the edges as curves without crossings that lead from one region's vertex, across a shared boundary segment, to an adjacent region's vertex. Conversely any planar graph can be formed from a map in this way. In graph-theoretic terminology, the four-color theorem states that the vertices of every planar graph can be colored with at most four colors so that no two adjacent vertices receive the same color, or for short:

Every planar graph is four-colorable.^[5]

Reference

^ From Gonthier (2008): "Definitions: A planar map is a set of pairwise disjoint subsets of the plane, called regions. A simple map is one whose regions are connected open sets. Two regions of a map are adjacent if their respective closures have a common point that is not a corner of the map. A point is a corner of a map if and only if it belongs to the closures of at least three regions. Theorem: The regions of any simple planar map can be colored with only four colors, in such a way that any two adjacent regions have different colors."
^ Swart (1980).
^ Wilson (2014), 216–222.
^ Hudson (2003).
^ Thomas (1998, стр. 849); Wilson (2014)).

Literatura

Allaire, Frank (1978), „Another proof of the four colour theorem. I.”, Ур.: D. McCarthy; H. C. Williams, Proceedings, 7th Manitoba Conference on Numerical Mathematics and Computing, Congr. Numer., 20, Winnipeg, Man.: Utilitas Mathematica Publishing, Inc., стр. 3—72, ISBN 0-919628-20-6, MR 0535003
Appel, Kenneth; Haken, Wolfgang (1977), „Every Planar Map is Four Colorable. I. Discharging”, Illinois Journal of Mathematics, 21 (3): 429—490, MR 0543792, doi:10.1215/ijm/1256049011
Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), „Every Planar Map is Four Colorable. II. Reducibility”, Illinois Journal of Mathematics, 21 (3): 491—567, MR 0543793, doi:10.1215/ijm/1256049012
Appel, Kenneth; Haken, Wolfgang (октобар 1977), „Solution of the Four Color Map Problem”, Scientific American, 237 (4), стр. 108—121, Bibcode:1977SciAm.237d.108A, doi:10.1038/scientificamerican1077-108
Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Contemporary Mathematics, 98, With the collaboration of J. Koch., Providence, RI: American Mathematical Society, ISBN 0-8218-5103-9, MR 1025335, doi:10.1090/conm/098
Bar-Natan, Dror (1997), „Lie algebras and the four color theorem”, Combinatorica, 17 (1): 43—52, MR 1466574, arXiv:q-alg/9606016  , doi:10.1007/BF01196130
Bernhart, Frank R. (1977), „A digest of the four color theorem”, Journal of Graph Theory, 1 (3), стр. 207—225, MR 0465921, doi:10.1002/jgt.3190010305
Borodin, O. V. (1984), „Solution of the Ringel problem on vertex-face coloring of planar graphs and coloring of 1-planar graphs”, Metody Diskretnogo Analiza (41): 12—26, 108, MR 832128 .
Cayley, Arthur (1879), „On the colourings of maps”, Proc. Royal Geographical Society, Blackwell Publishing, 1 (4), стр. 259—261, JSTOR 1799998, doi:10.2307/1799998
Fritsch, Rudolf; Fritsch, Gerda (1998), The Four Color Theorem: History, Topological Foundations and Idea of Proof, Translated from the 1994 German original by Julie Peschke., New York: Springer, ISBN 978-0-387-98497-1, MR 1633950, doi:10.1007/978-1-4612-1720-6
F. G. (10. 6. 1854), „Tinting Maps”, The Athenaeum: 726 .
Gonthier, Georges (2005), A computer-checked proof of the four colour theorem (PDF), unpublished
Gonthier, Georges (2008), „Formal Proof—The Four-Color Theorem” (PDF), Notices of the American Mathematical Society, 55 (11): 1382—1393, MR 2463991
Hadwiger, Hugo (1943), „Über eine Klassifikation der Streckenkomplexe”, Vierteljschr. Naturforsch. Ges. Zürich, 88: 133—143
Heawood, P. J. (1890), „Map-Colour Theorem”, Quarterly Journal of Mathematics, Oxford, 24, стр. 332—338
Hudson, Hud (мај 2003), „Four Colors Do Not Suffice”, The American Mathematical Monthly, 110 (5): 417—423, JSTOR 3647828, doi:10.2307/3647828
Kempe, A. B. (1879), „On the Geographical Problem of the Four Colours”, American Journal of Mathematics, the Johns Hopkins University Press, 2 (3): 193—220, doi:10.2307/2369235
Magnant, C.; Martin, D. M. (2011), „Coloring rectangular blocks in 3-space”, Discussiones Mathematicae Graph Theory, 31 (1): 161—170, doi:10.7151/dmgt.1535
McKay, Brendan D. (2012), A note on the history of the four-colour conjecture, Bibcode:2012arXiv1201.2852M, arXiv:1201.2852 
Nash-Williams, C. St. J. A. (1967), „Infinite graphs—a survey”, Journal of Combinatorial Theory, 3 (3): 286—301, MR 0214501, doi:10.1016/s0021-9800(67)80077-2 .
O'Connor; Robertson (1996), The Four Colour Theorem, MacTutor archive
Pegg, Ed, Jr.; Melendez, J.; Berenguer, R.; Sendra, J. R.; Hernandez, A.; Del Pino, J. (2002), „Book Review: The Colossal Book of Mathematics” (PDF), Notices of the American Mathematical Society, 49 (9): 1084—1086, Bibcode:2002ITED...49.1084A, doi:10.1109/TED.2002.1003756
Reed, Bruce; Allwright, David (2008), „Painting the office”, Mathematics-in-Industry Case Studies, 1: 1—8
Ringel, G.; Youngs, J.W.T. (1968), „Solution of the Heawood Map-Coloring Problem”, Proc. Natl. Acad. Sci. USA, 60 (2), стр. 438—445, Bibcode:1968PNAS...60..438R, PMC 225066  , PMID 16591648, doi:10.1073/pnas.60.2.438
Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1996), „Efficiently four-coloring planar graphs”, Proceedings of the 28th ACM Symposium on Theory of Computing (STOC 1996), стр. 571—575, MR 1427555, doi:10.1145/237814.238005
Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1997), „The Four-Colour Theorem”, J. Combin. Theory Ser. B, 70 (1), стр. 2—44, MR 1441258, doi:10.1006/jctb.1997.1750
Saaty, Thomas; Kainen, Paul (1986), „The Four Color Problem: Assaults and Conquest”, Science, New York: Dover Publications, 202 (4366): 424, Bibcode:1978Sci...202..424S, ISBN 0-486-65092-8, doi:10.1126/science.202.4366.424
Swart, Edward Reinier (1980), „The philosophical implications of the four-color problem”, American Mathematical Monthly, Mathematical Association of America, 87 (9), стр. 697—702, JSTOR 2321855, MR 0602826, doi:10.2307/2321855
Thomas, Robin (1998), „An Update on the Four-Color Theorem” (PDF), Notices of the American Mathematical Society, 45 (7), стр. 848—859, MR 1633714
Thomas, Robin (1995), The Four Color Theorem
Tietze, Heinrich (1910), „Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen” [Some remarks on the problem of map coloring on one-sided surfaces], DMV Annual Report, 19: 155—159
Thomas, Robin (1999), „Recent Excluded Minor Theorems for Graphs”, Ур.: Lamb, John D.; Preece, D. A., Surveys in combinatorics, 1999, London Mathematical Society Lecture Note Series, 267, Cambridge: Cambridge University Press, стр. 201—222, ISBN 0-521-65376-2, MR 1725004, doi:10.1017/CBO9780511721335
Tait, P. G. (1880), „Remarks on the colourings of maps”, Proc. R. Soc. Edinburgh, 10: 729, doi:10.1017/S0370164600044643
Wilson, Robin (2014) [2002], Four Colors Suffice, Princeton Science Library, Princeton, NJ: Princeton University Press, ISBN 978-0-691-15822-8, MR 3235839

Spoljašnje veze

Hazewinkel Michiel, ур. (2001). „Four-colour problem”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
Weisstein, Eric W. „Blanuša snarks”. MathWorld.
Weisstein, Eric W. „Map coloring”. MathWorld.
List of generalizations of the four color theorem on MathOverflow

[1] From Gonthier (2008): "Definitions: A planar map is a set of pairwise disjoint subsets of the plane, called regions. A simple map is one whose regions are connected open sets. Two regions of a map are adjacent if their respective closures have a common point that is not a corner of the map. A point is a corner of a map if and only if it belongs to the closures of at least three regions. Theorem: The regions of any simple planar map can be colored with only four colors, in such a way that any two adjacent regions have different colors."

[FOOTNOTESwart1980-2] Swart (1980).

[FOOTNOTEWilson2014216–222-3] Wilson (2014), 216–222.

[FOOTNOTEHudson2003-4] Hudson (2003).

[5] Thomas (1998, стр. 849); Wilson (2014)).

[1]

[2]

[3]

[4]

[5]