Радикс стабло

У рачунарству, радикс стабло (или компактно префикс стабло) је просторно оријентисана структура података у којој се сваки чвор са само једним дететом спојио са својим дететом. Резултат је да сваки унутрашњи чвор има најмање двоје деце. За разлику од редовних префиксних стабала, ивице могу бити означене са секвенцама елемената, као и појединачним елементима. То их чини много ефикаснијим за мале скупове(посебно ако су ниске дуге) и за групе ниски које имају дуже префиксе.

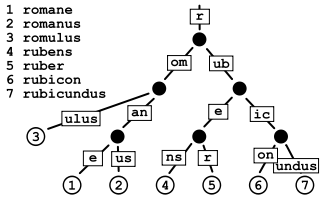
Као оптимизација, ознаке ивица могу бити смештене у сталној величини(за прве и последње елементе).^[1]

Имајте на уму да, иако су примери у овом чланку показују ниске као секвенце карактера, тип ниски у низу елемената може бити произвољно изабран (на пример, као бит или бајт репрезентације ниски када се користи кодирање са карактером од више битова или Уникод).

Употреба

Као што је поменуто, радикс стабла су корисна за изградњу асоцијативних низова са кључевима који се могу изразити као ниске. Налазе посебну примену у области ИП рутирања, где је могућност да садрже велике опсеге вредности, са пар изузетака, посебно погодна у хијерархијској организацији ИП адреса^[2]. Они се такође користе за инвертовано обележавање текстуалних докумената у преузимању информација.

Операције

Радикс стабла подржавају уметање, брисање и претраживање операције. Убацивање додаје нову ниску у стабло док у исто време покушава да смањи количину података који су додавани. Брисање уклања ниску од стабла. Претраживање операције укључује тачно проналажење, наћи претходника, наћи наследника, и пронаћи све ниске са префиксом. Све ове операције су О(k) где је k максимална дужина свих ниски у сету. Овај списак не може бити коначан.

Проналажење

Проналажење ниске у радикс стаблу

Операција проналажења утврђује да ли ниска постоји у стаблу. Већина операција мења овај приступ на неки начин да би се решили своје специфичне задатке. На пример, чвор где ниска престаје може бити од значаја. Ова операција је слична префикс стаблу осим што неке ивице конзумирају више елемената.

Следећи псеудо код претпоставља да ове класе постоје.

Ивица

Чвор targetNode
ниска label

Чвор

Низ ивица edges
функција isLeaf()

function lookup(string x)
{
  // Почети у корену без пронађених елемената
  Node traverseNode := root;
  int elementsFound := 0;
  
  // Пролазити док се не нађе лист или није могуће наставити
  while (traverseNode != null && !traverseNode.isLeaf() && elementsFound < x.length)
  {
    // Узети следећу ивицу за истраживање на основу елемената који још нису пронађени у Х
    Edge nextEdge := select edge from traverseNode.edges where edge.label is a prefix of x.suffix(elementsFound)
      // x.suffix(elementsFound) враћа задњи (x.length - elementsFound) елемент од x
  
    // Да ли је пронађена ивица?
    if (nextEdge != null)
    {
      // Ставити следећи чвор да се истражује
      traverseNode := nextEdge.targetNode;
    
      // Повећавати пронађене елементе на основу ознака постављених код ивица
      elementsFound += nextEdge.label.length;
    }
    else
    {
      // Прекинути петљу
      traverseNode := null;
    }
  }
  
  // Подударност је пронађена ако стигнемо до чвора листа и искоришћено је тачно x.length елемената
  return (traverseNode != null && traverseNode.isLeaf() && elementsFound == x.length);
}

Уношење

Да бисте унели ниску, тражимо дрво док се не може направити никакав даљи напредак. У овом тренутку можемо или додати нову одлазећу ивицу означену са свим преосталим елементима у улазну ниску, или ако већ постоји одлазећи ивица која дели префикс са преосталим улазним стрингом, можемо их поделити на две ивице (први означен са заједничким префиксом) и наставити. Ово раздвајање осигурава да ниједан чвор нема више деце него што има могућих елемената стринга.

Неколико случајева убацивања су приказани испод, мада још постоји. Имајте на уму да r једноставно представља корен. Претпоставља се да ивице могу бити означене са празним нискама да прекину ниске где је то потребно и да корен нема долазну ивицу.

Унети 'water' у корен
Унети 'slower' док се одржава 'slow'
Унети 'test' што је префикс од 'tester'
Унети 'team' док се раздваја 'test' и креира нова ознака ивице 'st'
Унети 'toast' док се раздваја 'te' и помера претходна ниска на нижи ниво

Брисање

Да бисте избрисали х стринг са стабла, прво пронађите лист који представља х. Затим, под претпоставком да постоји х, уклонимо одговарајући чвор листа. Ако родитељ нашег чвора листа има само једно друго дете, онда та долазна ознака детета се додаје родитељској надолазећој ознаци и дете се уклони.

Додатне операције

Пронаћи све низове са заједничким префиксом: Враћа низ ниски који почињу истим префиксом.
Пронаћи претходника: лоцира највећу ниску мању од задатог низа, по лексикографском поретку.
Пронаћи наследника: Проналази најмању ниску већу од задатог низа, по лексикографском поретку.

Историја

Доналд Р. Морисон(Donald R. Morrison) први је описао оно што је он назвао "Патрициа дрвеће" 1968-е,^[3] назив потиче од акронима Патрициа, што је скраћеница за "Практични алгоритам претраживања информација кодирана алфанумерички". Гернот Гвехенбергер(Gernot Gwehenberger) самостално је изумео и описао структуру података у отприлике исто време.^[4]

Поређење са другим структурама података

(У следећим поређењима, претпоставља се да су кључеви дужине k и структура података садржи n чланова.)

За разлику од само-балансирајућих стабала, радикс стабла дозвољавају проналажење, уметање, брисање и у времену О(k), а не О(log n). Ово не изгледа као предност, јер нормално k ≥ log n, али у балансираном стаблу свако поређење је поређење ниски које захтева О(k) у најгорем случају, од којих су многи у пракси спори због дугих заједничких префикса (у случају где поређење почне на почетку ниске). У префикс стаблу, ова поређења захтевају константно време, али је потребно m поређења да се пронађе низ дужине m. Радикс стабла може да обавља ове операције са мање поређења, и захтева много мање чворова.

Радикс стабла такође деле мане префикс стабала, ипак: као што се они могу применити само на низове елемената или елементе са ефикасним повратним мапирањем низова, немају потпуну општост избалансираних претраживања дрвећа, који се односе на било који тип података са укупно наручивања. Обртно мапирање за ниске може да се користи за производњу потребне тоталне наруџбине за балансирану претрагу дрвећа, али не и обрнуто. Ово такође може бити проблематично уколико тип података само пружа поређење операције, али не (де)серијализацију операција.

Код хеш табела се обично каже да је очекивано О(1) пута убацивања и брисања, али то важи само када је у питању обрачунавање хеш кључева да буде константа временска операција. Када се хешинг кључа узима у обзир, за хеш табеле се очекује О(k) пута убацивања и брисања, али може да траје дуже у најгорем случају у зависности од тога како се рукује са сударима. Радикс стабла имају најгори случај О(k) убацивања и брисања. Наследник/претходник операције радикс стабала се такође не спроводе преко хеш табеле.

Варијанте

Заједнички продужетак радикс стабала користи две боје чворова, "црне" и "беле“. Да бисте проверили да ли дата ниска се чува у дрвету, претраживање почиње од врха и прати ивице улазне ниске док се напредак не може више остварити. Ако се тражена ниска конзумира и коначни чвор је црни чвор, претраживање није успело, а ако је беле боје, претрага је успела. То нам омогућава да додамо велики асортиман ниски са заједничким префиксом у стабло, користећи беле чворове, а затим уклонити мали скуп "изузетака" просторски ефикасним начином убацивања помоћу црних чворова.

Референце

^ Morin, Patrick. „Data Structures for Strings” (PDF). Приступљено 15. 4. 2012.
^ Knizhnik, Konstantin. "Patricia Tries: A Better Index For Prefix Searches", Dr. Dobb's Journal, June, 2008.
^ Morrison, Donald R. Practical Algorithm to Retrieve Information Coded in Alphanumeric
^ G. Gwehenberger, Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968), pp. 223–226

Спољашње везе

Algorithms and Data Structures Research & Reference Material: PATRICIA, by Lloyd Allison, Monash University
Patricia Tree, NIST Dictionary of Algorithms and Data Structures
Crit-bit trees, by Daniel J. Bernstein
Radix Tree API in the Linux Kernel, by Jonathan Corbet
Kart (key alteration radix tree), by Paul Jarc

[1] Morin, Patrick. „Data Structures for Strings” (PDF). Приступљено 15. 4. 2012.

[2] Knizhnik, Konstantin. "Patricia Tries: A Better Index For Prefix Searches", Dr. Dobb's Journal, June, 2008.

[3] Morrison, Donald R. Practical Algorithm to Retrieve Information Coded in Alphanumeric

[4] G. Gwehenberger, Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968), pp. 223–226

[1]

[2]

[3]

[4]