Цилиндрична еквивалента пројекција

У картографији је цилиндрична еквивалентна пројекција дио породице цилиндричних пројекција.

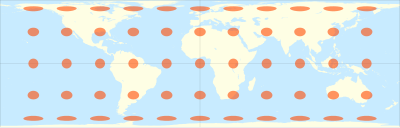
Цилиндричне пројекције

Израз "нормална цилиндрична пројекција" користи се за означавање било које пројекције у којој се меридијани пресликавају у једнако размакнуте вертикалне линије, а кругови географске ширине у хоризонталне линије (или, линије геодетског датума, уопштено говорећи, картирају се радијалне линије са фиксне тачке на једнако размакнуте паралелне линије и концентричне кругове које се пресликавају се окомите линије). Цилиндричне пројекције су једне од најкоришћенијих пројекција, али нису толико популарне као цилиндричне конформне пројекције.

Картирање меридијана као вертикалних линија може се визуализовати замишљањем цилиндра (чија се оса поклапа са Земљином осом ротације или обртном осом) који обмотава Земљу и затим да се Земљина сфера пројектује на цилиндар, а затим се тако пројектовани цилиндар одмотава у раван.

Геометријом своје конструкције цилиндричне пројекције се протежу у правцу исток-запад. Размјера истезања је иста на било којој изабраној географској ширини на свим цилиндричним пројекцијама, а дата је секантом географске ширине као производом размјере екватора. Различите цилиндричне пројекције међусобно се разликују само по свом истезању у правцу сјевер-југ (гдје је географска ширина дата са φ):

Једине цилиндричне пројекције које чувају однос подручја имају компресију у правцу сјевер-југ, која је управо реципрочна истезању у правцу исток-запад ( cos φ ): цилиндрична еквивалентна пројекицја (са многим специјализованим пројекцијама као што су Гал-Петерсова или Галова ортографска пројекција, Берманова и Ламбертова цилиндрична еквивалента пројекција). Ово дјели дистанце у правцу сјевер-југ са фактором једнаким секанту географске ширине, чувајући површине, али озбиљно искривљујући облике, тј. углове.

Свака карта у цилиндричној еквивалентној пројекцији је једнаке површине и има пар идентичних географских ширина супротног предзнака (или екватора) на којима се размјера исток-запад поклапа са размјером сјевер-југ.

Опис

Формуле

Све цилиндричне еквивалентне пројекције користе формулу:

{\begin{aligned}x&=(\lambda -\lambda _{0})\cos \varphi _{0}\\y&={\frac {\sin \varphi }{\cos \varphi _{0}}}\end{aligned}}

где је λ географска дужина, λ ₀ је централни меридијан, φ је географска ширина, а φ ₀ је стандардна ширина, ^[1] гдје су све вриједности изражене у радијанима.

Неки картографи више воле да раде у степенима, а не у радијанима, и користе еквивалентну формулу:

{\begin{aligned}x&={\frac {\pi (\lambda -\lambda _{0})\cos \varphi _{0}}{180^{\circ }}}\\y&={\frac {\sin \varphi }{\cos \varphi _{0}}}\end{aligned}}

Поједностављене формуле

Уклањањем јединице конверзије и уједначеним скалирањем, формуле се могу написати у сљедећем облику:

{\begin{aligned}x&=(\lambda -\lambda _{0})S\\y&=\sin \varphi \end{aligned}}

Стога се сфера пресликава на растегнути вертикални цилиндар или ваљак. Фактор деформације S је оно што разликује варијације цилиндричне еквивалентне пројекције.

Разматрања

Различите специјализације цилиндричне еквивалентне пројекције разликују се само у односу вертикалне и хоризонталне осе пројекицје. Овај однос одређује стандардну паралелу пројекције, а то је паралела на којој нема деформација и дуж које растојања на сфери одговарају наведеној размјери, тј. однос мора бити 1. На цилиндричној еквивалентној пројекцији увијек постоје две стандардне паралеле, свака на истој удаљености сјеверно и јужно од екватора. Стандардне паралеле Гал-Петерсове пројекције су 45° N и 45° S. Неколико других специјализација еквидистантних цилиндричних пројекција је описано или другачије именовано у картографији. ^[2] ^[3] ^[4] ^[5] ^[6]

Именоване специјализације цилиндричне еквивалентне пројекције
Пројекција	Аутор (година)	Стандардне паралеле на сјеверу и југу	Однос ширине и висине
цилиндрична еквивалентна пројекција (основна пројекција за све остале)		φ ₀	$π$ (cos φ₀)²
Ламбертова	Јохан Хајнрих Ламберт (1772)	Екватор (0°)	$π$ ≈ 3.142
Берманoва	Валтер Берман (1910)	30°	3π / 4 ≈ 2.356
Смит еквивалентна = Крастер правоугаона	Чарлс Пијаци Смит (1870)	$\arccos {\sqrt {\tfrac {2}{\pi }}}$ ≈ 37° 04′17 ″	2
Тристан Едвардсова	Тристан Едвардс (1953)	37° 24 ′	≈ 1.983
Хобо–Дајерова	Мик Дајер (2002)	37° 30 ′	≈ 1.977
Гал–Петерсова = Галова ортографкса =Петерсова	Џејмс Гал (1855) промовисано од Арно Петерса као његов сопствени изум (1967)	45°	π / 2 ≈ 1.571
Балтасартова	М. Балтасартова (1935)	50°	≈ 1.298
Тоблеровова пројекција на квадрату	Валдо Тоблер (1986)	$\arccos {\sqrt {\tfrac {1}{\pi }}}$ ≈ 55° 39′14 ″	1

Референце

^ Map Projections – A Working Manual Архивирано 2010-07-01 на сајту Wayback Machine, USGS Professional Paper 1395, John P. Snyder, 1987, pp.76–85
^ Snyder, John P. (1989). An Album of Map Projections p. 19. Washington, D.C.: U.S. Geological Survey Professional Paper 1453. (Mathematical properties of the Gall–Peters and related projections.)
^ Monmonier, Mark (2004). Rhumb Lines and Map Wars: A Social History of the Mercator Projection p. 152. Chicago: The University of Chicago Press. (Thorough treatment of the social history of the Mercator projection and Gall–Peters projections.)
^ Smyth, C. Piazzi. (1870). On an Equal-Surface Projection and its Anthropological Applications. Edinburgh: Edmonton & Douglas. (Monograph describing an equal-area cylindric projection and its virtues, specifically disparaging Mercator's projection.)
^ Weisstein, Eric W. "Cylindrical Equal-Area Projection." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CylindricalEqual-AreaProjection.html
^ Tobler, Waldo and Chen, Zi-tan(1986). A Quadtree for Global Information Storage. http://www.geog.ucsb.edu/~kclarke/Geography232/Tobler1986.pdf

[1] Map Projections – A Working Manual Архивирано 2010-07-01 на сајту Wayback Machine, USGS Professional Paper 1395, John P. Snyder, 1987, pp.76–85

[Snyder2-2] Snyder, John P. (1989). An Album of Map Projections p. 19. Washington, D.C.: U.S. Geological Survey Professional Paper 1453. (Mathematical properties of the Gall–Peters and related projections.)

[Monmonier-3] Monmonier, Mark (2004). Rhumb Lines and Map Wars: A Social History of the Mercator Projection p. 152. Chicago: The University of Chicago Press. (Thorough treatment of the social history of the Mercator projection and Gall–Peters projections.)

[Smyth-4] Smyth, C. Piazzi. (1870). On an Equal-Surface Projection and its Anthropological Applications. Edinburgh: Edmonton & Douglas. (Monograph describing an equal-area cylindric projection and its virtues, specifically disparaging Mercator's projection.)

[5] Weisstein, Eric W. "Cylindrical Equal-Area Projection." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CylindricalEqual-AreaProjection.html

[Tobler_and_Chen-6] Tobler, Waldo and Chen, Zi-tan(1986). A Quadtree for Global Information Storage. http://www.geog.ucsb.edu/~kclarke/Geography232/Tobler1986.pdf

[1]

[2]

[3]

[4]

[5]

[6]