Steinhaus-Johnson-Trotter algoritam

Steinhaus–Johnson–Trotter algoritam ili Johnson–Trotter algoritam (engl. Steinhaus–Johnson–Trotter algorithm) je algoritam koji je dobio ime po Hugu Štajnhausu, Selmeru M. Džonsonu i Haleu F. Troteru koji generiše sve permutacije od n elemenata. Svaka permutacija u nizu se razlikuje od prethodne po tome što su joj neka dva susedna elementa zamenila mesta. Ovaj algoritam takođe pronalazi Hamiltonov put u permutoedru (engl. Permutohedron).

Hamiltonov put (engl. Hamiltonian path) u Kejlijevom grafu (engl. Cayley graph) simetrične grupe generisane Steinhaus–Johnson–Trotter algoritmom

Ova metoda je još u 17. veku bila poznata engleskim zvonarima (engl. change ringing), a Sedgewick 1977 ju je nazvao "verovatno najistaknutijim algoritmom za generisanje permutacija". Osim što je jednostavan i računski efikasan, ovaj algoritam ima prednost u tome što se izračunavanje svake sledeće permutacije može ubrzati zbog velike sličnosti između uzastopnih permutacija.

Rekurzivna struktura

Niz permutacija n brojeva se može konstruisati od niza permutacija n - 1 brojeva tako što se broj n stavlja na svaku moguću poziciju u svakoj od kraćih permutacija. Ako je permutacija od n - 1 elemenata parna permutacija(engl. parity of a permutation) (što važi za prvu, treću itd. permutaciju u nizu) onda se broj n postavlja na svaku moguću poziciju u opadajućem poretku u toj permutaciji, od n do 1. Kada je permutacija od n - 1 elemenata neparna, broj n se postavlja na svaku moguću poziciju u rastućem poretku.

Dakle, kod permutacije od jednog elementa,

1

broj 2 ćemo postaviti na svaku moguću poziciju u opadajućem poretku i tako formirati dve permutacije od dva elementa,

1 2

2 1

Nakon toga broj 3 možemo postaviti na svaku moguću poziciju u opadajućem poretku u prvoj permutaciji "1 2", i u rastućem poretku u permutaciji "2 1":

1 2 3

1 3 2

3 1 2

3 2 1

2 3 1

2 1 3

U sledećem koraku rekurzije, broj 4 će biti postavljan u opadajućem poretku u permutaciju 1 2 3, u rastućem poretku u permutaciju 1 3 2, u opadajućem poretku u permutaciju 3 1 2, itd. Isti način postavljanja elementa n, naizmenično rastući i opadajući, se primenjuje za svaki broj veći od n. Ovim se dobija da se svaka permutacija razlikuje od prethodne ili pomeranjem n-a za jednu poziciju ili po promeni dva manja broja nasleđena iz kraće permutacije. U svakom slučaju, ova razlika u stvari predstavlja samo zamenu dva susedna elementa. Kada je n > 1, prva i poslednja permutacija u nizu se takođe razlikuju samo na dva susedna mesta, što se može dokazati indukcijom.

Iako se permutacije mogu generisati rekurzivnim algoritmom koji najpre formira niz manjih permutacija a zatim izvršava sva moguća ubacivanja najvećeg broja na rekurzivan način, Steinhaus-Johnson-Trotter algoritam izbegava rekurziju i formira niz permutacija iterativnom metodom.

Algoritam

Kako je to opisao Johnson 1963, ovaj algoritam za generisanje sledeće permutacije od zadate permutacije π, izvršava sledeće korake:

• Za svako i od 1 do n, neka je x_i pozicija gde je vrednost i smeštena u permutaciji π. Ako niz brojeva od 1 do i - 1 u permutaciji π definiše parnu permutaciju onda je y_i = x_i - 1, a inace y_i = x_i + 1.

• Pronalazi se najveći broj i za koji y_i predstavlja validnu poziciju u permutaciji π koja sadrži broj manji od i. Zameniti vrednosti na pozicijama x_i i y_i.

Ako nije moguće pronaci broj i takav da bude zadovoljen uslov drugog koraka, algoritam je došao do poslednje permutacije u nizu i prestaje sa radom. Ova procedura se može obaviti u vremenu O(n) po permutaciji.

Trotter 1962 je dao alternativnu implementaciju iterativnog algoritma za isti niz permutacija u nekomentarisanom pseudokodu (engl. pseudocode).

Pošto ova metoda generiše permutacije koje su naizmenično parne i neparne, ona se može lako izmeniti tako da generiše samo parne ili samo neparne permutacije: za generisanje sledeće permutacije iste parnosti, treba primeniti istu proceduru dva puta.

Even-ovo ubrzanje

Poboljšanje koje je uveo Shimon Even smanjuje brzinu izvršavanja algoritma tako što čuva dodatne informacije o svakom elementu u permutaciji: njegovu poziciju i smer (pozitivan, negativan ili nula) u kome se trenutno kreće (to je suštinski ista informacija u poređenju sa parnošću permutacije u verziji algoritma koju je definisao Johnson). Inicijalno, smer broja 1 je nula, a svi ostali elementi imaju negativan smer:

1 -2 -3

U svakom koraku, algoritam pronalazi najveći element čiji je smer različit od nule i zamenjuje mu mesto sa susednim elementom u smeru u kome pokazuje:

1 -3 -2

Ako ovaj korak dovede do toga da se tekući element nađe na prvoj ili poslednjoj poziciji u permutaciji, ili ako je susedni element u istom smeru veći od tekućeg elementa, njegov smer se postavlja na nulu:

3 1 -2

Posle svakog koraka, svi elementi veći od tekućeg imaju pozitivne ili negativne smerove, u zavisnosti od toga da li se nalaze između tekućeg elementa i početka permutacije (pozitivan) ili između tekućeg elementa i kraja permutacije (negativan). Dakle, u ovom primeru, nakon pomeranja broja 2, broju 3 biva ponovo dodeljen smer:

+3 2 1

Preostala dva koraka algoritma za n = 3 su:

2 +3 1

2 1 3

Algoritam prestaje sa radom kada svi elementi postanu neoznačeni.

Ovaj algoritam se izvršava za O(i) vremena za svaki korak u kome je najveći broj za pomeranje n - i + 1. Prema tome, zamene koje se vrše nad brojem n traju konstantno vreme. Pošto ove zamene čine tek 1/n-ti deo svih zamena koje izvrši algoritam, prosečno vreme po permutaciji je takođe konstantno, iako će mali broj permutacija koštati više vremena.

Kompleksnija verzija ovog algoritma koja ne sadrži petlje (engl. loopless algorithm) omogućava da se generisanje svake pojedinačne permutacije izvršava u konstantnom vremenu, ali modifikacije potrebne da se eliminišu petlje ga čine sporijim u praksi.

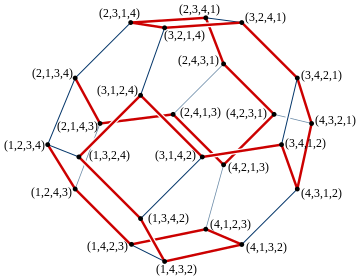
Geometrijska reprezentacija

Skup svih permutacija n elemenata geometrijski se može predstaviti pomoću permutoedra, politopa (engl. polytope) formiranog iz konveksnih omotača n! vektora, permutacija vektora (1,2,...n). Iako je definisano u n-dimenzionom prostoru, zapravo je (n - 1)-dimenzioni politop; na primer permutoedar sa 4 elemenata je trodimenzioni poliedar, okrnjeni oktaedar (engl. truncated octahedron). Ako je svako teme permutoedra označeno inverznom permutacijom permutaciji definisanoj od strane koordinata temena, dobijeno označavanje opisuje Kejlijev graf simetrične grupe permutacija n elemenata, kao što je generisano od strane permutacija koje menjaju susedne parove elemenata. Svake dve uzastopne permutacije u nizu generisanom Steinhaus-Johnson-Trotter algoritmom odgovaraju na ovaj način dvoma temenima koji formiraju završne tačke ivice u permutoedru i ceo niz permutacija opisuje Hamiltonov put u permutoedru, put koji svakim temenom prolazi tačno jednom. Ukoliko je niz permutacija završen dodavanjem još jedne ivice iz poslednje permutacije u prvu u nizu, rezultat je Hamiltonov ciklus.

Veza sa Grejovim kodom

Grejov kod (Gray code) za brojeve u datoj osnovi je niz koji sadrži brojeve do određene granice, tako da se parovi uzastopnih brojeva razlikuju za tačno jednu cifru. n! permutacija n brojeva od 1 do n može da se dovede u jedan na jedan predstavljanje sa n! brojeva od 0 do n! - 1 tako što se svaka permutacija uparuje sa sekvencom brojeva c_i koji broji broj pozicija u permutaciji koje su desno od vrednosti i i koje sadrže vrednosti manje od i (tj, broj inverzija gde je i veće od druge vrednosti) i interpretiranje ovih nizova brojeva u faktorijelnom brojevnom sistemu (engl. factorial number system). Na primer permutacija (3,1,4,5,2) daje vrednosti c₁ = 0, c₂ = 0, c₃ = 2, c₄ = 1, c₅ = 1. Niz (0,0,2,1,1) daje broj

0 × 0! + 0 × 1! + 2 × 2! + 1 × 3! + 1 × 4! = 34.

Uzastopne permutacije u nizu generisane Steinhaus-Johnson-Trotter algoritmom imaju broj inverzija koje se razlikuju za jednu cifru, formirajući Grejov kod za faktorijelni brojevni sistem.

Uopšteno, istraživači kombinatornih algoritama su definisali Grejov kod za skup kombinatornih objekata gde su objekti poređani jedan do drugog tako da se razlikuju na najmanji mogući način. U ovom generalizovanom slučaju Steinhaus-Johnson-Trotter algoritam generiše Grejov kod za same permutacije.

Istorijat

Algoritam je nazvan po Hugo Steinhaus, Selmer M. Johnson i Hale F. Trotter. Džonson i Troter su nezavisno jedan od drugog osmislili algoritam u ranim šezdesetim. Štajhausova knjiga, prvobitno objavljena 1958, a na engleski prevedena 1963. opisuje povezanu slagalicu generisanja svih permutacija pomoću sistema čestica, gde se svaka čestica kreće konstantnom brzinom duž linije i gde jedna čestica preuzima mesto druge. Nije moguće rešenje za n > 3, pošto je broj zamena daleko manji od broja permutacija, ali Steinhaus-Johnson-Trotter algoritam opisuje kretanje čestica sa nekonstantnom brzinom koja generiše sve permutacije.

Izvan matematike, isti metod je poznat mnogo duže za promenu zvonjave crkvenih zvona: metod opisuje postupak po kome skup crkvenih zvona zvoni po svim mogućim permutacijama, menjajući redosled samo dva zvona po promeni. Ove takozvane jednostavne promene su zabeležene 1621. za 4 zvona, a kasnije je Fabijan Stedman (Fabian Stedman) u svojoj knjizi izlistao rešenja za do 6 zvona. U skorije vreme, poštuje se pravilo da nijedno zvono ne može da ostane u istoj poziciji tri uzastopne permutacije; ovo pravilo je prekršeno od strane jednostavnih promena, tako da su osmišljene nove strategije koje menjaju više zvona odjednom.

Reference

• Dershowitz, Nachum (1975), „A simplified loop-free algorithm for generating permutations”, Nordisk Tidskr. Informationsbehandling (BIT), 15 (2): 158—164, doi:10.1007/bf01932689 .
• Dijkstra, Edsger W. (1976), „On a gauntlet thrown by David Gries” (PDF), Acta Informatica, 6 (4): 357—359, doi:10.1007/BF00268136 . Although DIjkstra does not cite any prior literature, an earlier draft EWD502 reveals that he knew of Trotter 1962.
• Ehrlich, Gideon (1973), „Loopless algorithms for generating permutations, combinations, and other combinatorial configurations”, Journal of the ACM, 20 (3): 500—513, doi:10.1145/321765.321781 .
• Even, Shimon (1973), Algorithmic combinatorics, Macmillan .
• Johnson, Selmer M. (1963), „Generation of permutations by adjacent transposition”, Mathematics of Computation, 17: 282—285, JSTOR 2003846, doi:10.1090/S0025-5718-1963-0159764-2 .
• Knuth, Donald (2011), „Section 7.2.1.2: Generating All Permutations”, The Art of Computer Programming, volume 4A, Архивирано из оригинала 30. 03. 2012. г., Приступљено 01. 06. 2015 .
• McGuire, Gary (2003), Bells, motels and permutation groups, CiteSeerX: 10.1.1.6.5544 .
• Savage, Carla (1997), „A survey of combinatorial Gray codes”, SIAM Review, 39 (4): 605—629, JSTOR 2132693, doi:10.1137/S0036144595295272 .
• Sedgewick, Robert (1977), „Permutation generation methods”, ACM Comput. Surv., 9 (2): 137—164, doi:10.1145/356689.356692 .
• Steinhaus, Hugo (1964), One hundred problems in elementary mathematics, New York: Basic Books, стр. 49—50 .
• Trotter, H. F. (avgust 1962), „Algorithm 115: Perm”, Communications of the ACM, 5 (8): 434—435, doi:10.1145/368637.368660 .

Spoljašnje veze

• Counting And Listing All Permutations: Johnson–Trotter Method at cut-the-knot
• Reference Java implementation of an iterator implemeting the Evens' speedup algorithm at sourceforge