Батервортов филтер
Батервортов филтер је тип филтра који има равну опадајучу карактеристику, у пропусном опсегу и сматра се компромисом између Чебишевог и Беселовог филтра. Филтер је назван по Британском инжињеру Стивену Батерворту (Stephen Butterworth) који га је први описао 1930. године.


Уопштено
уредиОвај термин се више односи на тип одзива него на специфичан тип филтра. Преносна функција се тако димензионише да нема „таласања“ у пропусном опсегу и опада према нули у непропусном[1]. Ово се постиже изједначавањем извода преносне функције са нулом, на централној учестаности филтра (то је нпр. нула за нископропусне филтре).
Овдје ћу детаљније обрадити нископропусне, високопропусне као и филтре пропуснике опсега, у случају кад је дато коло нижег или коло вишег реда. Филтри првог реда су они код којих одзив опада 6dB по октави (20dB по декади). Код филтера другог реда, ријеч је о -12 dB/оцт, док се код трећег реда ради о -18/оцт.
Дизајн филтра
уредиПостоје неколико различитих топологија, односно врста израде овог линеарног, аналогног филтра. Најкориштеније су Кауерова и Сален-Ки топологије.
Сален-Ки топологија
уредиСален-Ки топологија користи активне и пасивне компоненте (углавном су то операциони појачавачи, отпорници и кондензатори). Сваки степен Сален-Кија додаје по пар полова. На крају се сви степени филтра повежу редно.[2]
Анализа генеричког примјера
уредиСа слике се види да је код ОП-а затворена негативна спрега па је стога V-=V+=Vout. Напишимо једначину за чвор X:
или:
Струја је иста кроз елементе Z2 и Z4 па је очигледно:
Из чега добијамо
Уврстимо ли то у једначину за чвор X, добијамо:
Из чега добијамо преносну функцију:
Ако би компонента Z3 била уземљена, филтер би био дјелитељ напона (на Z1 и Z3), каскадно везан са дјелитељем напона на Z2 и Z3.
Зависно од одабира пасивних компоненти за (отпорника и кондензатора) може се добити нископропусни, високопропусни или филтер пропусник опсега.
Примјер анализе нископропусног филтра
уредиЗа амортизацију (као бафер) се користи ОП, али се такође може користити и БЈТ емитер . Компоненте су одабране на сљедећи начин: З1=Р1; З2=Р2; З3=1/(сЦ1); З4=1/(сЦ2) .
Уврштавањем ових вриједности у израз за преносну функцију који смо добили у претходном случају, добијамо:
Да би задовољили општу формулу:
сводимо на:
из чега се лако закључи да је:
- тј. : Такође се добија да је :
представља цутофф фреквенцију ( наравно цутофф кружну учестаност), док је фактор доброте (бездимензиона величина) који описује колико је висок и широк пик одзива филтра. Већи Q фактор означава мањи губитак енергије у односу на фреквенцију, тј. осцилације се спорије гасе (одумиру).
Дизајнер мора одабрати параметре и зависно од ситуације. Напримјер, Батервортов филтер другог реда, који има највећи флет одзив у пропусном опсегу, има који износи . Имамо 2 параметра за подешавање, а 4 непознате (), обично се узима један отпорник као однос са другим (типа ). Исто се уради и код одабира кондендзатора.
Примјер одабира елемената
уреди
Коло са слике има од 15.9 кХз и фактор од 0.5. Преносна функција изгледа овако:
Послије уврштавања (; ), добијамо:
Одавде видимо да се једноставном промјеном односа Р,C или м,н може постићи иста фреквенција и фактор доброте за било који филтер.
Примјер анализе високопропусног филтра
уреди
Анализираћемо високопропусни филтер другог реда, са слике. Његова преносна функција ће бити облика:
Из једначина:
Сређивањем се добија:
Упоређивањем једначина се добија:
Примјер анализе филтра пропусника опсега
уреди
На слици је приказан бандпасс филтер имплементиран у ВЦВС топологији. Иако није иста топологија, метод анализе је сличан и лакше га је објаснити на овом примјеру. Преносна функција овог филтра је дата изразом:
Централна учестаност (фреквенција гдје одзив има свој пик) се добија изразом:
Напонски дјељитељ у колу са негативном повратном спрегом контролише гејн. "Унутрашњи гејн" од операционог појачавача је
док је гејн појачавача, на фреквенцији пика, дат изразом:
Видимо да се мора држати испод 3 да филтер не би осцилирао. Филтер се обично оптимизује одабиром и .
Буттерwортх филтри вишег реда
уредиРед филтра је број његових полова и који ћемо употријебити, зависи од практичне потребе. Активан филтер са Н полова има роллофф рате од Н x 6дБ/октави (Н x 20дБ/декади). Слично, одзив високопропусног филтра са Н полова повецава се по Н x 6дБ/октави, све до цутофф фреквенције. У оба случаја, ф_ц је дефинисано као:
Магнитуда напонске преносне функције за нископропусне филтре N-тог реда је:

За високопропусне филтре N-тог реда, магнитуда напонске преносне функције је:
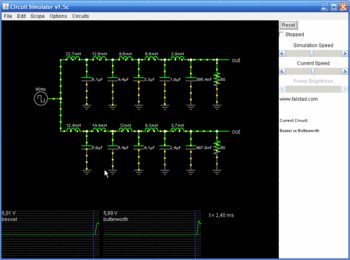
На слици је приказан нископропусни Батервортов филтер трећег реда (има 3 пола). Три отпорника су једнака а однос између капацитивности тако што се први и други извод преносне функције изједначе са нулом.
Филтри вишег реда се могу конструисати додавањем још RC мрежа. Међутим, ефекат пуњења за сваку додатну RC мрежу постаје све видљивији. Ово се превазилази тако што се каскадно (редно) вежу филтри другог реда са ОП-ом (значи сваки филтер има по један ОП у себи).Због ниске излазне отпорности ОП-а, готово да нема ефекта пуњења између каскада. Примјер таквог филтра се може видјети на слици. Максимално раван одзив се не добија простим везивањем на ред ових дво-полних филтера. Потребно је ускладити капацитивности изједначавањем прва три извода функције преноса, са нулом. На сличан начин се могу конструисати и филтри вишег реда. Пропусници и непропусници опсега користе сличну конфигурацију.
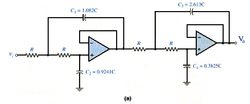
Примјер рјешавања нископропусног активног Буттерwортх филтра трећег реда
уредиОд разних топологија које су нам на располагању за израду филтра вишег реда, Саллен-Кеy захтијева најмањи број компоненти па је такав филтер лакше анализирати (нпр. само један ОП за 3-полни одзив 18 dB/oct). Слиједи опис анализе склопа са слике 6.
Посматрамо чвор 3b (гдје је v3 = v3a = v3b). Једначина за напон чвора се може написати и овако:
Означимо: Затим:
Напони за остале чворове гласе:
Преносна функција H(s) = Vout/Vin, сада изгледа H(s)=
Примијетимо да је општи облик за H(s) 3-полног Буттерwортх нископропусног филтра на цутофф фреквенцији од 1 рад/сец:
Примијетимо:
гдје је Кац = M.
Изаберемо излазни раст од: Kac = 3 (9,5 dB)
Такође, изаберемо сљедеће вриједности компоненти:
Рјешавајучи по R1, R2, R3 и R4 dobijamo:
- R1= 816.46 Om, R2= 481.26 Om, R3= 848.33 Om, R4= 10 kOm
Дозвољено нам је да промијенимо вриједности Р1-Р4 према ЕИА стандарду од 1% толеранције по декади:
- R1= 825 Om, R2= 487 Om, R3= 845 Om, R4= 20 kOm
Практични савјети:
- За различите вриједности раста могу се користити вриједности компоненти са табеле испод, или сваки блок засебно рјешавати за различиту вриједност Кац. Користите само позитивне позитивне поткорјене вриједности. Програмски пакет Mathcad(TM) може помоћи при рачуну.
| M(Kac) | 0dB | 6dB | 12dB | 18dB | 24dB | 30dB | 36dB |
|---|---|---|---|---|---|---|---|
| R1(Ω) | 1.292 | 15.652 | 1.624 | 4.305 | 3.246 | 1.437 | 3.234 |
| R2(Ω) | 2.093 | 14.694 | 4.067 | 1.750 | 2.134 | 16.260 | 7.198 |
| R3(Ω) | 3.698 | 4.348 | 15.144 | 13.276 | 1.444 | 42.794 | 42.950 |
| R4(Ω) | 0 | 10.000 | 30.000 | 70.000 | 15.000 | 31.000 | 63.000 |
| R5(Ω) | ∞ | 10.000 | 10.000 | 10.000 | 1.000 | 1.000 | 1.000 |
| C1(F) | 10-3 | 10-4 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 |
| C2(F) | 10-3 | 10-4 | 10-4 | 10-4 | 10-4 | 10-5 | 10-5 |
| C3(F) | 10-4 | 10-4 | 10-4 | 10-4 | 10-3 | 10-4 | 10-4 |
| M(Kac) | 42dB | 48dB | 54dB | 60dB | 66dB | 72dB | 78dB |
|---|---|---|---|---|---|---|---|
| R1(Ω) | 1.640 | 1.242 | 2.243 | 1.030 | 1.137 | 1.700 | 6.053 |
| R2(Ω) | 13.615 | 69.066 | 32.123 | 185.004 | 285.242 | 136.553 | 47.723 |
| R3(Ω) | 4.479 | 116.556 | 138.815 | 5.249 | 308.473 | 430.832 | 346.170 |
| R4(Ω) | 127.000 | 25.500 | 51.100 | 102.300 | 20.470 | 40.950 | 81.910 |
| R5(Ω) | 1.000 | 100 | 100 | 100 | 10 | 10 | 10 |
| C1(F) | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 |
| C2(F) | 10-5 | 10-6 | 10-6 | 10-6 | 10-7 | 10-7 | 10-7 |
| C3(F) | 10-3 | 10-4 | 10-4 | 10-3 | 10-4 | 10-4 | 10-4 |
Примјер трополног Батервортовог филтра
уреди
У приказаној шеми:
- 1. Транзистори Мм6, 7, 8, 9 и 10 су транзистори за струјно огледало у шеми за мјешач.
- 2. Први транскондуктор чине Mf1 и 2 (и активно оптерећење). Он се понаша као заштита између мјешача и филтра.
- 3. Rf1 и Cf1 су два од уређаја који се користе у нормализованом нископропусном филтру (подешеном на фреквенцију и импедансу)
- 4. Четири транскондукторске ћелије (Mf2-10 и одговарајућа активна оптерећења) и кондензатор Cf2 чине активни индуктор.
- 5. Рф2 и Цф3 су крајње компоненте нормализованог нископропусног филтра.
Мрежа за помјерање фазе има централну фреквенцију од 5,5 MHz и пропусни опсег (гдје је фазни помак линеаран) од око 1 MHz. То је у суштини паралелна RLC мрежа гдје је индуктор активни индуктор.

У горњој шеми:
- 1. Кондензатори Cps1 и 2 су изабрани тако да је њихова реактанса једнака реактанси Rps1.
- 2. R је изабрано тако да одређени фактор доброте Q (и потом ширину пропусног опсега фазно помјерајуће мреже).
- 3. Cps3 и активни индуктор (двије транскондукторске ћелије) подешавају централну фреквенцију у мрежи за помјерање фазе.
Кауер топологија
уреди
Кауер топологија користи пасивне компоненте (кондензаторе и калемове) за имплементацију линеарног аналогног филтра. Израз за k-ти елемент је дат у форми:
- ; к = непарно
- ; к = парно
Филтер се може реализовати и са серијски везаним индуктивитетом на почетку, али се у том случају узима да је Lk од k непарно а Ck од k парно.
Референце
уреди- ^ Гиованни Бианцхи анд Роберто Соррентино (2007). Елецтрониц филтер симулатион & десигн. МцГраw-Хилл Профессионал. стр. 17–20. ИСБН 9780071494670.
- ^ Доналд А Неамен (2009). Мицроелецтроницс Цирцуит Аналyсис анд Десигн. МцГраw-Хилл. стр. 1050-1070. ISBN 978-0-07-338064-3, 9780073380643.
Литература
уреди- Доналд А Неамен (2009). Мицроелецтроницс Цирцуит Аналyсис анд Десигн. МцГраw-Хилл. стр. 1050-1070. ISBN 978-0-07-338064-3, 9780073380643.
- Giovanni Bianchi and Roberto Sorrentino (2007). Electronic filter simulation & design. McGraw-Hill Professional. стр. 17–20. ISBN 9780071494670.
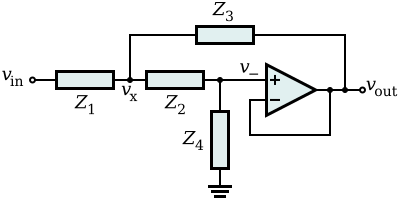


















































![{\displaystyle {\frac {\frac {M}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}{\left[s^{3}+\left({\frac {1}{R_{1}\cdot C_{1}}}+{\frac {1}{R_{2}\cdot C_{1}}}+{\frac {1}{R_{2}\cdot C_{2}}}+{\frac {1-M}{R_{3}\cdot C_{3}}}+{\frac {1}{R_{3}\cdot C_{2}}}\right)\cdot s^{2}+\left({\frac {R_{3}\cdot C_{3}+R_{1}\cdot C_{3}+R_{2}\cdot C_{3}+C_{1}\cdot R_{1}+\left(1-M\right)\cdot \left(R_{1}+R_{2}\right)\cdot C_{2}}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}\right)\cdot s+{\frac {1}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e8ee843fec7366eeb49552f53d163f3b10cfc6d)







