Експоненцијална расподела

У теорији вероватноће и статистици, експоненцијална расподела (позанта као негативна експоненцијална расподела) је расподела вероватноће времена између догађаја у Поасоновом процесу, и.е., процесу у коме се догађаји континуирано и независно јављају са константном просечном брзином. То је посебан случај гама дистрибуције. Експоненцијална дистрибуција је континуирани аналог геометријске дистрибуције и има кључно својство да је без меморије. Поред тога што се користи за анализу Поасонових тачкастих процеса, она се јавља у мноштву других контекста.

Експоненцијална

Функција густине вероватноће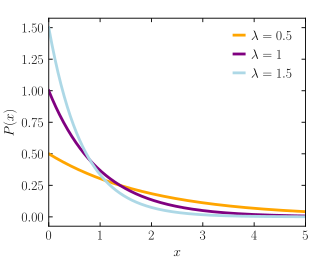
Функција кумулативне расподеле
Параметри	λ > 0 стопа, или инверзна скала
Носитељ	x ∈ [0, ∞)
ПДФ	λ е−λx
ЦДФ	1 − е−λx
Квантил	−лн(1 − Ф) / λ
Просек	λ−1 (= β)
Медијана	λ−1лн(2)
Модус	0
Варијанса	λ−2 (= β2)
Коеф. асиметрије	2
Куртоза	6
Ентропија	1 − лн(λ)
МГФ	${\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda$
ЦФ	${\frac {\lambda }{\lambda -it}}$
Фишерова информација	$\lambda ^{-2}$
Кулбек-Лајблерова дивергенција	$D_{KL}(\exp _{0}\parallel \exp _{1})=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1$

Експоненцијална дистрибуција није исто што и класа експоненцијалне фамилије дистрибуција, која је велика класа дистрибуција вероватноће којом је обухваћена експоненцијална дистрибуција као један од њених чланова, али такође укључује нормалну дистрибуцију, биномну дистрибуцију, гама дистрибуцију, Поасонову, и многе друге.

Карактеризација

Функција густине вероватноће

Функција густине вероватноће експоненцијалне дистрибуције је

$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Алтернативно, ово се може дефинисати коришћењем десне-континуиране Хевисајдове одскочне функције, Х(x) где је Х(0) = 1:

$f(x;\lambda )=\lambda e^{-\lambda x}H(x)$

Овде је λ > 0 параметер дистрибуције, који се обично назива параметар брзине. Дистрибуција је подржана на интервалу [0, ∞). Ако случајна променљива X има ову дистрибуцију, пише се X ~ Еxп(λ).

Експоненцијална дистрибуција испољава бесконачну дељивост.

Функција кумулативне дистрибуције

Функција кумулативне дистрибуције је дата са

$F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Алтернативно, ово се може дефинисати користећи Хевисајдову одскочну функцију, Х(x).

$F(x;\lambda )=\mathrm {(} 1-e^{-\lambda x})H(x)$

Алтернативна параметризација

Најчешће коришћена алтернативна параметризација је путем дефинисања функције густине вероватноће (пдф) експоненцијалне дистрибуције као што је

$f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-{\frac {x}{\beta }}}&x\geq 0,\\0&x<0.\end{cases}}$

где је β > 0 средња вредност, стандардна девијација, и параметар скале дистрибуције, реципрочна вредност параметра брзине, λ, дефинисаног изнад. У овој спецификацији, β је параметар преживљавања у смислу да ако је случајна варијабла X временско трајање током кога одређени биолошки или механички систем успе да преживи и X ~ Еxп(β), онда је Е[X] = β. Наиме, очекивано трајање преживљавања система је β јединица времена. Параметризација која укључује параметар „брзине” настаје у контексту догађаја који пристижу брзином λ, када време између догађаја (које се може моделовати користећи експоненцијалну дистрибуцију) има средњу вредност β = λ⁻¹.

Алтернативна спецификација је понекад подеснија од горе наведене, а неки аутори је користе као стандардну дефиницију. Ова алтернативна спецификација се овде не користи. Нажалост, то доводи до нејасноћа у нотацијама. Генерално, читалац мора проверити која се од ове две спецификације користи, ако аутор пише „X ~ Еxп(λ)”, мисли се било на нотацију из претходне секције (користећи λ) или на нотацију из ове секције (овде, користећи β да се изегне забуна).

Особине

Средња вредност, варијанса, моменти и медијана

Средња вредност је центар масе вероватноће, односно први моменат.

Медијана је прасликавање Ф⁻¹(1/2).

Средња или очекивана вредност експоненцијално распоређене случајне променљиве X са параметром брзине λ је дата са

$$\operatorname {E} [X]={\frac {1}{\lambda }}.$$

У светлу доле наведених примера, ово има смисла: ако се примају телефонски позиви у просеку два пута на сат, онда се може очекивати да ће се чекати пола сата на сваки позив.

Варијанца од X је дата са

$$\operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},$$

тако да је стандардна девијација једнака са средњом вредношћу.

Моменти од X, за $n\in \mathbb {N}$ су дати са

$$\operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.$$

Централни моменти од X, за $n\in \mathbb {N}$ су дати са

$$\mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.$$

где је !н подфакторијал од н

Медијана од X је дата са

$$\operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],$$

где се лн односи на природни логаритам. Стога је апсолутна разлика између средње вредности и медијане

$$\left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],$$

у складу са средњом вредности неједнакост.

Својство непамћења експоненцијалне случајне променљиве

Експоненцијално распоређена случајна променљива Т поштује однос

$$\Pr \left(T>s+t\mid T>s\right)=\Pr(T>t),\qquad \forall s,t\geq 0.$$

Ово се може видети ако се узме у обзир комплементарна кумулативна функција дистрибуције:

$${\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}$$

Када се Т тумачи као време чекања да се догађај деси у односу на неко почетно време, ова релација имплицира да, ако је Т условљено неуспехом да се посматра догађај током неког почетног временског периода с, дистрибуција преосталог времена чекања је исто што и оригинална безусловна расподела. На пример, ако се догађај није догодио након 30 секунди, условна вероватноћа да ће за догађај бити потребно још најмање 10 секунди једнака је безусловној вероватноћи посматрања догађаја више од 10 секунди након почетног времена.

Експоненцијална расподела и геометријска расподела су једине расподеле вероватноће без меморије.

Експоненцијална расподела је стога нужно и једина континуирана расподела вероватноће која има константну стопу неуспеха.

Квантили

Тукијеви критеријуми за аномалије.

Функција квантила (инверзна кумулативна функција расподеле) за Еxп(λ) је

$$F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1$$

Према томе, квартили су:

• први квартил: лн(4/3)/λ
• медијана: лн(2)/λ
• трећи квартил: лн(4)/λ

Као последица тога, интерквартилни опсег је лн(3)/λ.

Условна вредност под ризиком (очекивани недостатак)

Условна вредност под ризиком (ЦВаР) такође позната као очекивани недостатак или суперквантил за Еxп(λ) се изводи на следећи начин:

$${\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}$$

Буферована вероватноћа прекорачења (бПОЕ)

Баферована вероватноћа прекорачења је један минус ниво вероватноће на коме је ЦВаР једнак прагу $x$. Изводи се на следећи начин:

$${\begin{aligned}{\bar {p}}_{x}(X)&=\{1-\alpha |{\bar {q}}_{\alpha }(X)=x\}\\&=\{1-\alpha |{\frac {-\ln(1-\alpha )+1}{\lambda }}=x\}\\&=\{1-\alpha |\ln(1-\alpha )=1-\lambda x\}\\&=\{1-\alpha |e^{\ln(1-\alpha )}=e^{1-\lambda x}\}=\{1-\alpha |1-\alpha =e^{1-\lambda x}\}=e^{1-\lambda x}\end{aligned}}$$

Кулбацк–Либлерова дивергенција

Усмерена Кулбак–Либлерова дивергенција у натима од $e^{\lambda }$ („приближна“ дистрибуција) од $e^{\lambda _{0}}$ („права“ дистрибуција) даје

$${\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}$$

Максимална расподела ентропије

Међу свим континуираним расподелама вероватноће са подршком на [0, ∞) и средњом вредношћу μ, експоненцијална расподела са λ = 1/μ има највећу диференцијалну ентропију. Другим речима, то је максимална дистрибуција вероватноће ентропије за случајну променљиву X која је већа или једнака нули и за коју је Е[X] фиксно.

Литература

• Б. С. Еверитт (2006). Тхе Цамбридге Дицтионарy оф Статистицс (3рд изд.). Цамбридге: Цамбридге Университy Пресс. ИСБН 978-0-521-69027-0. 
• Бисхоп (2006). Паттерн Рецогнитион анд Мацхине Леарнинг. Спрингер. ИСБН 978-0-387-31073-2. 
• ден Деккер, А. Ј.; Сијберс, Ј. (2014). „Дата дистрибутионс ин магнетиц ресонанце имагес: А ревиеw”. Пхyсица Медица. 30 (7): 725—741. ПМИД 25059432. дои:10.1016/ј.ејмп.2014.05.002. 
• Сунг Нок Цхиу; Стоyан, Диетрицх; Wилфрид С. Кендалл; Мецке, Јосепх (27. 6. 2013). Стоцхастиц Геометрy анд Итс Апплицатионс. Јохн Wилеy & Сонс. ИСБН 978-1-118-65825-3. 
• Ј. Ф. C. Кингман (17. 12. 1992). Поиссон Процессес. Цларендон Пресс. ИСБН 978-0-19-159124-2. 
• Пиерре Симон де Лаплаце (1812). Аналyтицал Тхеорy оф Пробабилитy. 
• А. Колмогорофф (1933). Грундбегриффе дер Wахрсцхеинлицхкеитсрецхнунг. ИСБН 978-3-642-49888-6. дои:10.1007/978-3-642-49888-6. 
• Биллингслеy, Патрицк (1979). Пробабилитy анд Меасуре. Неw Yорк, Торонто, Лондон: Јохн Wилеy анд Сонс. 
• Олав Калленберг; Фоундатионс оф Модерн Пробабилитy, Спрингер Сериес ин Статистицс.. 650 пп. (2nd изд.). 2002. ISBN 978-0-387-95313-7. 
• Тијмс, Хенк (2004). Ундерстандинг Пробабилитy. Цамбридге Университy Пресс. 
• Олав Калленберг; Пробабилистиц Сyмметриес анд Инварианце Принциплес. Спрингер -Верлаг, Неw Yорк. 510 пп. 2005. ISBN 978-0-387-25115-8.
• Гут, Аллан (2005). Пробабилитy: А Градуате Цоурсе. Спрингер-Верлаг. ИСБН 978-0-387-22833-4. 

Спољашње везе

• Хазеwинкел Мицхиел, ур. (2001). „Еxпонентиал дистрибутион”. Енцyцлопаедиа оф Матхематицс. Спрингер. ISBN 978-1556080104. 
• Online calculator of Exponential Distribution