Усмерени граф

У математици, а посебно у теорији графова, усмерени граф или диграф је граф или скуп чворова повезаних гранама, где гране имају правац. У формалном смислу, усмерен граф-то је уређен пар G = (V, A) (понекад у ознаци G = (V, E)).

• V је  скуп чији се елементи зову врхови, чворови, или тачке;
• А(понекад и Е) је скуп уређених парова чворова, које се називаоју стрелицама, усмереним гранама (понекад само гранама са одговарајућим скупом по имену Е уместо A),или усмерене линије.

Усмерени граф.

Усмерени граф са одговарајућом матрицом суседства

Он се разликује од обичног или неусмереног графа, у томе што је неусмерени граф дефинисан као скуп двоелементних скупова чворова, који се обично називају гране или линије.

Усмерени граф се зове прост диграф , ако између никоја два различита чвора не постоји више од једне усмерене гране и ако нема петље (гране које повезују чвор са самим собом). Усмерени граф се зове усмерени мултиграф или мултидиграф ако он може да има неколико стрела (а понекад и циклусе). У овом другом случају, гране формирају мултискуп, а не скуп, уређених парова чворова.

Основни појмови

Грана (x,y) сматра се усмереном од чвора x до чвора y; Y се зове глава а x се зове реп гране (стрелице); Y је директан следбеник од x-a,  а x је директан претходник од y. Ако пут води од x-а ка y код, y је следбеник од x и достижан (могуће је стићи до тог чвора) од x. X је претходник y-a. Грана (y,x) се зове обрнутом граном (x,y).

Додајући оријентацију неодређеном графу, тј постављајучи смер сваке гране, од обичног графа добијамо усмерен граф. Било који граф који се направи на овакав начин назива се оријентисан граф. Међу усмереним графовима, оријентисајни графови су они који немају 2 циклуса (највише једна грана (x,y) и једна грана (y,x) могу бити гране графа).

Тежински усмерени граф је усмерени граф са одређеним тежинама (вредностима) које се додају уз сваку грану, сличан је као тежински граф.

У контексту теорије графова, тежински усмерени граф се често називамрежом.

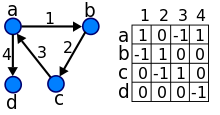
Матрица суседства мултидиграфа који има циклусе, је матрица са целим вредностима, редовима и колонама који одговарају чворовима, где је недијагонално пољe а_ij - број грана од чвора i до чвора ј, a дијагонално пољеа_ii - број циклуса у чвору i.

Још једно матрично приказивање графа је његова матрица учесталости.

Улазни и излазни степен

Усмерени граф, са означеним чворовима (улазни степен, излазни степен).

Улазни степен чвора (u)  у ознаци deg-(u) представља број грана којима је чвор u завршни чвор. Излазни степен чвора (u) у ознаци deg+(u) представља број грана којима је чвор u почетни чвор.

Нека је G = (V, E) и v∈V. Чвор који има deg-(u)=0 назива се извором, и он је порекло свих осталих инцидентних грана.

Слично томе, чвор који има deg+(v)=0 назива се понор.

Ако чвор није ни извор , ни понор, тада се он зове унутрашњи.

Формула за степен чвора у усмереном графу је

${\displaystyle }$

Ако за сваки чвор важи v∈V, deg+(v) = deg−(v), тада се тај граф назива балансиран оријентисан граф.

Низ степена

Низ степена директног графа је низ парова, његових улазних и излазних степена, за пример који је горе наведен, имамо низ степена ((2, 0), (2, 2), (0, 2), (1, 1)). Два графа су изоморфна ако имаји исти низ степена, мада понекад се може десити да графови иако нису изоморфни имају исти низ степена

Проблем реализације графа је задатак проналажења усмереног графа са задатим низом степена који су дати у облику целобројних парова. Низ, који је низ степена неког усмереног графа, односно за који проблем реализације усмереног графа има решење, зове се усмерени граф или усмерен графички низ. Овај проблем може бити решен уз помоћ Клеитман–Ван алгоритма или уз помоћ Фулкерсон–Чен–Анстее теореме.

Повезаност усмереног графа

Усмерен граф је слабо повезан (или само повезан), ако је неусмерен основни граф, добијен заменом свих грана у директном графу са неусмереним гранама,повезан граф. Усмерен граф је јако повезан или јак, ако садржи директан пут из у чвор y, и директан пут из чвора y до чвора x, за сваки пар чворова (x,y). Јаке компоненте су најјачи повезани подграфови.

Класе усмереног графа

Симетрични диграф је усмерени граф у коме свака грана која њему припада, има своју инверзну грану, која такође њему припада. Симетричан, безцикличан усмерен је еквивалентан графу са гранама замењеним са паром инверзних грана. Број неусмерених грана је једнак половини броју усмерених грана.

Једноставан оријентисан ацикличан граф.

Усмерен ацикличан граф је усмерен граф без усмерених циклуса. Посебан случај усмерених ацикличних графова, су  мултистабла (графови у којима не постоји пут тако да се из почетног чвора врати назад до тог истог чвора), оријентисано стабло или полистабло (усмерени графови добијени усмеравањем свих грана неусмереног ацикличног стабла) и кореново стабло (оријентисане стабло, у коме је један чвор означен као корен, тј почетан чвор).

Турнир на 4 врха.

Турнир - је оријентисан граф добијен тако што се бира смер сваке гране у неусмереном потпуном графу.

Види још

• Дијаграм тока
• Теорија графова
• Граф тока (математика)
• Оријентација (теорија графова)
• Сигнални ток графа
• Вертикално ограничен граф

Литература

• Bang-Jensen, Jørgen; Gutin, Gregory (2000). directed graphs: Theory, Algorithms and Applications. Springer. ISBN 978-1-85233-268-6. 
  (ревидиран 1-ог издања 2007. године, сада слободно доступан на аутора сајта; 2. издање појавио у 2009, ISBN 1-84800-997-6).
• Bondy, John Adrian; Murty, U. S. R. (1976). Graph Theory with Applications. North-Holland. ISBN 978-0-444-19451-0. Архивирано из оригинала 13. 04. 2010. г. Приступљено 25. 06. 2016. .
• Diestel, Reinhard (2005). Graph Theory (3rd изд.). Springer. ISBN 978-3-540-26182-7.  (електронски 3. издање је слободно доступан на сајту аутора).
• Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley .
• Број циљу тачкама (или графа) са врхова од онлајн Енциклопедије Интегер секвенци