Сигмоидна функција
Сигмоидна функција или сигмоид је математичка функција која има карактеристичну криву у облику латиничног слова „S” или сигмоидну криву. Често се израз сигмоидна функција односи на посебан облик логистичке функције приказан на првој слици и дефинисан једначином .

Међу посебним случајевима сигмоидне функције су Гомперцова крива (која се користи у системима моделовања који сатурирају на великим вредностима -a) и оуџи крива (која се користи у преливу неких брана). Сигмоидне функције имају домен свих реалних бројева, а повратна вредност се монотоно повећава најчешће између 0 и 1 или, алтернативно, од -1 до 1, у зависности од конвенције.
Широк спектар сигмоидних функција, међу којима су логистичке и хиперболичне тангентне функције, користе се као активациона функција вештачких неурона. Сигмоидне криве су такође уобичајене у статистици као кумулативне функције расподеле (које иду од 0 до 1), као што су интеграли логистичке расподеле, нормалне расподеле и студентске функције густине вероватноће.
Дефиниција
уредиСигмоидна функција је ограничена, диференцијабилна, реална функција која је дефинисана за све реалне улазне вредности и има ненегативни извод у свакој тачки.[1]
Својства
уредиУ принципу, сигмоидна функција је монотона и има први извод који је у облику звона. Сигмоидна функција је ограничена правом хоризонталних асимптота када .
Сигмоидна функција је конвексна за вредности мање од 0, а конкавна за вредности веће од 0. Због тога, сигмоидна функција и њене афине композиције могу имати вишеструке оптимуме.
Примери
уреди- Логистичка функција
- Хиперболички тангенс (померена и скалирана верзија логистичке функције изнад)
- Гудерманова функција
- Генерализована логистичка функција
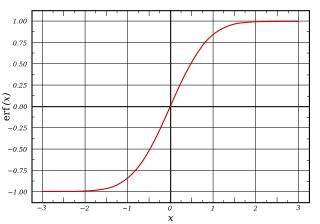
Интеграл било које непрекидне, ненегативне функције у облику чворуге ће бити сигмоидан, тако да су кумулативне функције расподеле за многе заједничке расподеле вероватноћа сигмоидне. Један такав пример је функција грешке, која је повезана са кумулативном функцијом расподеле нормалне расподеле.
Примене
уредиМноги природни процеси, као што су сложене системске криве учења, показују напредак од малих почетака који убрзавају и приближавају се врхунцу током времена. Када недостаје одређени математички модел, често се користи сигмоидна функција.[2] Ван Генучтен-Гуптин модел се заснива на обрнутој „S” кривој и примењује се на одговор приноса житарица на салинитет тла.
Референце
уреди- ^ From natural to artificial neural computation : International Workshop on Artificial Neural Networks, Malaga-Torremolinos, Spain, June 7-9, 1995 : proceedings. Mira, J. (José), Sandoval, Francisco. Berlin: Springer-Verlag. 1995. ISBN 9783540594970. OCLC 32548755.
- ^ Gibbs, M. N.; MacKay, D. C. (2000). „Variational Gaussian process classifiers”. IEEE transactions on neural networks. 11 (6): 1458—1464. ISSN 1045-9227. PMID 18249869. doi:10.1109/72.883477.


