Spinsko staklo

Spinsko staklo u fizici naziv je za magnetne materijale kod kojih je orijentacija magnetnih spinova neuređena. Izraz potiče iz analogije sa strukturom stakla, koja je amorfna, te je neuređena u odnosu na konfiguraciju kristalne rešetke.

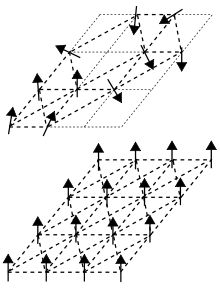
Spinsko staklo ima unutrašnju strukturu koja se nalazi u metastabilnom stanju, zato što je energija kod neuređene konfiguracije viša od energije osnovnog stanja, koja odgovara potpuno uređenom feromagnetnom stanju.

Interakcije između atoma u spinskom staklu su jako kompleksne, te se pri operativnom radu sa modelima spinskog stakla najčešće pretpostavlja da su orijentacije spinova slučajno određene.^[1]

Magnetne osobine spinskog stakla

Pri eksperimentalnom ispitivanju materijala sa neuređenom spinskom strukturom, uočena su neobična magnenta ponašanja. Susceptibilnost spinskih stakala zavisi od temperature relativno pravilno kao i paramagnetici do kritične temperature od nekoliko Kelvina. Ispod te temperature ponašanje nije bilo pravilno.

Na temperaturama iznad kritične, susceptibilnost ne zavisi od frekvencije, ali je utvrđeno i pravilno ponašanje susceptibilnosti na temperaturama nižim od kritične u vremenski promenljivim magnetnim poljima. S obzirom da susceptibilnost raste sa sve nižim vrednostima frekvencije, teorijski se očekuje da na kritičnoj temperaturi dolazi do faznog prelaza.

Edvard-Andersonov model

Edvard-Andersonovim modelom, Hamiltonijan spinskog sistema je pretpostavljen u obliku:

H=-\sum _{<ij>}J_{ij}S_{i}S_{j},

gde $S$ odgovara matrici spina atoma, a sumira se po najbližim susednim atomima u rešetki.

Vidi još

Reference

^ Statistička fizika, H. Hilhorst, 14. oktobar 2016.^{[mrtva veza]}

Literatura

Edwards, S.F.; Anderson, P.W. (1975). Theory of spin glasses. Journal of Physics F: Metal Physics. 5. str. 965—974. [1]
Sherrington, David; Kirkpatrick, Scott (1975). Solvable model of a spin-glass. Physical Review Letters. 35. str. 1792—1796. Bibcode:1975PhRvL..35.1792S. doi:10.1103/PhysRevLett.35.1792. Papercore Summary http://papercore.org/Sherrington1975 Arhivirano 2013-04-15 na sajtu Archive.today
Nordblad, P.; Lundgren, L.; Sandlund, L. (1986). A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses. Journal of Magnetism and Magnetic Materials. 54. str. 185—186. Bibcode:1986JMMM...54..185N. doi:10.1016/0304-8853(86)90543-3.
Binder, K.; Young, A. P. (1986). Spin glasses: Experimental facts, theoretical concepts, and open questions. Reviews of Modern Physics. 58. str. 801—976. Bibcode:1986RvMP...58..801B. doi:10.1103/RevModPhys.58.801.
Bryngelson, Joseph D.; Wolynes, Peter G. (1987). Spin glasses and the statistical mechanics of protein folding. Proceedings of the National Academy of Sciences. 84. str. 7524—7528. Bibcode:1987PNAS...84.7524B. doi:10.1073/pnas.84.21.7524.
Fischer, K. H.; Hertz, J. A. (1991). Spin Glasses. Cambridge University Press.
Mezard, Marc; Parisi, Giorgio; Virasoro, Miguel Angel (1987). Spin glass theory and beyond. Singapore: World Scientific. ISBN 978-9971-5-0115-0.
Mydosh, J. A. (1995). Spin Glasses. Taylor & Francis.
Parisi, G. (1980). The order parameter for spin glasses: a function on the interval 0-1. J. Phys. A: Math. Gen. 13. str. 1101—1112. Bibcode:1980JPhA...13.1101P. doi:10.1088/0305-4470/13/3/042. Papercore Summary http://papercore.org/Parisi1980 Arhivirano 2013-04-15 na sajtu Archive.today.
Talagrand, Michel (2000). Replica symmetry breaking and exponential inequalities for the Sherrington–Kirkpatrick model. Annals of Probability. 28. str. 1018—1062. JSTOR 2652978. doi:10.1214/aop/1019160325.
Guerra, F.; Toninelli, F. L. (2002). The thermodynamic limit in mean field spin glass models. Communications in Mathematical Physics. 230. str. 71—79. Bibcode:2002CMaPh.230...71G. arXiv:cond-mat/0204280  . doi:10.1007/s00220-002-0699-y.

Spoljašnje veze

[1] Statistička fizika, H. Hilhorst, 14. oktobar 2016.^{[mrtva veza]}

[1]