Funkcija raspodele prostih brojeva

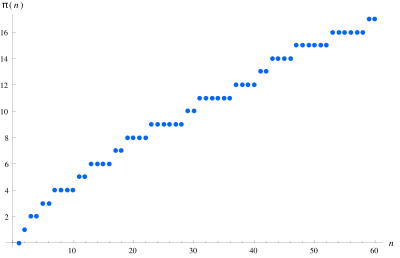
U matematici, funkcija raspodele prostih brojeva je funkcija raspodele broja prostih brojeva manjih ili jednakih nekoj stvarnom broju x. Označava se $\scriptstyle \pi (x)$ (nepovezani sa brojem π).

Vrednosti π(n) za prvih 60 celih brojeva

Istorija

Od velikog interesovanja u teoriji brojeva je stopa rasta funkcije raspodele prostih brojeva. To su pretpostavili krajem 18. veka Gaus i Ležandr da bude približno

$x/\operatorname {ln} (x)\!$

u smislu da

$\lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\operatorname {ln} (x)}}=1.\!$

Ovaj izraz je teorema prostih brojeva. Ekvivalentni izraz je

$\lim _{x\rightarrow \infty }\pi (x)/\operatorname {li} (x)=1\!$

gde jeli je logaritamska integralna funkcija. Teoremu prostih brojeva je prvi put dokazao 1896. godine Žak Adamard i Čarls de la Vale Puson samostalno, koristeći svojstva Rimanove zeta funkcije koju je uveo Riman 1859. godine.

Preciznije procene $\pi (x)\!$ koje su sada poznate; na primer

$\pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}\!$

gde je O je beleženje za veliko O. Za većinu vrednosti $x$ mi smo zainteresovani za (to jest, kada $x$ nije nerazumno veliki) $\operatorname {li} (x)\!$ je veći od $\pi (x)\!$, ali beskrajno često je suprotno. Za raspravu o tome, pogledaj Skjuesov broj.

Dokazi o teoremi prostih brojeva ne koriste zeta funkciju ili složene analize koje su pronađeni oko 1948. godine Atl Selberg i Pol Erdoš(u najvećoj meri nezavisno).

Tabele π(x), x / ln x, i li(x)

Tabela prikazuje kako su tri funkcije π(x), x / ln x i li(x) upoređujuće na stepen 10. Vidi još,id

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)
10	4	−0.3	2.2	2.500
102	25	3.3	5.1	4.000
103	168	23	10	5.952
104	1,229	143	17	8.137
105	9,592	906	38	10.425
106	78,498	6,116	130	12.740
107	664,579	44,158	339	15.047
108	5,761,455	332,774	754	17.357
109	50,847,534	2,592,592	1,701	19.667
1010	455,052,511	20,758,029	3,104	21.975
1011	4,118,054,813	169,923,159	11,588	24.283
1012	37,607,912,018	1,416,705,193	38,263	26.590
1013	346,065,536,839	11,992,858,452	108,971	28.896
1014	3,204,941,750,802	102,838,308,636	314,890	31.202
1015	29,844,570,422,669	891,604,962,452	1,052,619	33.507
1016	279,238,341,033,925	7,804,289,844,393	3,214,632	35.812
1017	2,623,557,157,654,233	68,883,734,693,281	7,956,589	38.116
1018	24,739,954,287,740,860	612,483,070,893,536	21,949,555	40.420
1019	234,057,667,276,344,607	5,481,624,169,369,960	99,877,775	42.725
1020	2,220,819,602,560,918,840	49,347,193,044,659,701	222,744,644	45.028
1021	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	47.332
1022	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	49.636
1023	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	51.939
1024	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	54.243
1025	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	56.546
1026	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	58.850

Grafik pokazuje odnos funkcije raspodele prostih brojeva π(x)do dve svoje aproksimacije, x/ln x i Li(x). Kao x raste ( napomena x osa je logaritamska), oba odnosa naginju ka 1. Odnos za x/ln x konvergira odozgo vrlo sporo, dok je odnos za Li(x) konvergira brže odozdo.

U onlajn enciklopediji celih sekvenci, π(x)Kolona je sekvenca A006880 π(x) - x / ln x je sekvenc  A057835, i li(x) − π(x) je sekvenca  A057752.

Vrednost za π(10²⁴)su prvobitno izračunava J. Both, J. Franke, A. Džost, i T. Klejnjung pod pretpostavkom Rimanove hipoteze. Kasnije je proverio bezuslovnim izračunavanjem D. J. Plat. Za vrednost π(10²⁵)je zbog J. Both, J. Franke, A. Džost, i T. Kleinjung. Za vrednost π(10²⁶)izračunao je D. B. Stapl. Svi ostali upisi u ovoj tabeli su verifikovani kao delovi tog posla.

Algoritmi za vrednovanje π(x)

Jednostavan način da se pronađe $\pi (x)$, ako $x$ nije preveliko, je da se koristi Eratostenovo sito i proizvedu prosti brojevi manji ili jednaki$x$a zatim ih prebrojati.

Podrobniji način pronalaženja$\pi (x)$ je zbog Ležandreja: dato $x$, ako $p_{1},p_{2},\ldots ,p_{n}$ su različiti prosti brojevi, onda je broj celih brojeva manji ili jednak $x$koji su nedeljivi sa $p_{i}$ je

$\lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots$

(gde $\lfloor \cdots \rfloor$ označava sprat funkciju). Ovaj broj je stoga jednak

$\pi (x)-\pi \left({\sqrt {x}}\right)+1$

kada brojevi $p_{1},p_{2},\ldots ,p_{n}$ su prosti brojevi manji ili jednaki od kv.korena $x$.

U seriji tekstova objavljenih između 1870. i 1885. godine Ernest Mejsel opisuje (i koristi) praktičan način vrednovanja kombinatornog $\pi (x)$. Let $p_{1}$, $p_{2},\ldots ,p_{n}$ gde prvi $n$ prosti brojevi i označavaju strane $\Phi (m,n)$broj prirodnih brojeva ne veći o $m$ koji nisu deljiv sa $p_{i}$. Tada

$\Phi (m,n)=\Phi (m,n-1)-\Phi \left({\frac {m}{p_{n}}},n-1\right)$

Datje prirodan broj $m$, ako $n=\pi \left({\sqrt[{3}]{m}}\right)$ i ako $\mu =\pi \left({\sqrt {m}}\right)-n$, tada

$\pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)$

koristeći ovaj pristup, Mejsel je izračunao $\pi (x)$, za $x$ jednako 5×10⁵, 10⁶, 10⁷, i 10⁸.

Godine 1959, Derik Henri Lehmer je proširio i pojednostavio Mejselobu metodu. Definisati, za realan $m$ i za prirodne brojev $n$ i $k$, $P_{k}(m,n)$ kao broj brojeva nije veći od m sa tačno k prostim činiocem, boljim od $p_{n}$. Osim toga, komplet $P_{0}(m,n)=1$. Tada

$\Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)$

gde zbir zapravo ima samo konačno mnogo različitih od nula uslove. $y$označava ceo broj takav da je ${\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}$, i sklop $n=\pi (y)$. Tada $P_{1}(m,n)=\pi (m)-n$ i $P_{k}(m,n)=0$ kada $k$ ≥ 3. Stoga

$\pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)$

Proračun $P_{2}(m,n)$može se dobiti na ovaj način:

$P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right)$

S druge strane, računanje $\Phi (m,n)$ može biti urađeno koristeći sledeća pravila:

1. $\Phi (m,0)=\lfloor m\rfloor$
2. $\Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)$

Koristeći svoj metod i IBM 701, Lehmer je mogao da izračuna $\pi \left(10^{10}\right)$.

Dalji napredak ove metoda su napravili Lagarijas, Miler, Odlisko, Delegliz i Rivat.

Druge funkcije raspodele prostih brojeva

Druge funkcije raspodele prostih brojeva se koriste jer su pogodnije za rad. Jedna je Rimanova funkcija raspodele prostih brojeva, obično označena kao $\Pi _{0}(x)$ili $J_{0}(x)$. Ovaj skok 1/n za proste stepene pⁿ, uz to uzimanje vrednosti na pola puta između dve strane u diskontinuitetu. Detalj je dodat jer onda može biti definisan od strane suprotnosti. Melin ga je preobrazio. Formalno, možemo definisati $\Pi _{0}(x)$ kao

$\Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}$

gde je p prost broj. 

Moguće je i napisati

$\Pi _{0}(x)=\sum _{2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}(x^{1/n})$

gdeje Λ(n) von Mangoldotova funkcija i 

$\pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.$

Mebijusova inverzna formula daje

$\pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}(x^{1/n})$

Znajući odnos između Rimanove zeta funkcije i von Mangoldotove funkcije  $\Lambda$, i korišćenjem Peronove formule imamo

$\ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx$

Čebiševa funkcija težine prostih brojeva ili prostih stepena pⁿ od ln(p):

$\theta (x)=\sum _{p\leq x}\ln p$

$\psi (x)=\sum _{p^{n}\leq x}\ln p=\sum _{n=1}^{\infty }\theta (x^{1/n})=\sum _{n\leq x}\Lambda (n).$

Pimanova funkcija raspodele prostih brojeva ima običnu proizvodnu funkciju koja se može izraziti u smislu formalne serije stepena kao:

$\sum _{n=1}^{\infty }\Pi _{0}(n)x^{n}=\sum _{a=2}^{\infty }{\frac {x^{a}}{1-x}}-{\frac {1}{2}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }{\frac {x^{ab}}{1-x}}+{\frac {1}{3}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }{\frac {x^{abc}}{1*x}}-{\frac {1}{4}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }{\frac {x^{abcd}}{1-x}}+\cdots$

Formule za funkcije raspodele prostih brojeva

Formula za funkcije raspodele prostih brojeva se javljaju u dve vrste: aritmetičke formula i analitičke formula. Analitičke formule za raspodelu prostih brojeva bile su prvi put upotrebljene da se dokaže prosta teorema brojeva. One proizilaze iz Rimanovog i von Mangoldotovog rada, i opšte su poznata kao eksplicitne formule.

Imamo sledeći izraz za ψ:

$\psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})$

gde 

$\psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.$

Ovde ρ su nule Rimanova zeta funkcija u kritičnoj traci, gde je prava deli ρ je između nula i jedinice. Formula važi za vrednosti xveći od jedan, što je oblast interesovanja. Iznos po korenu je uslovno konvergira, a treba uzeti u cilju povećanja apsolutnu vrednost imaginarnog dela. Imajte na umu da istu suma nad trivijalnim korenovima daje poslednje oduzimanje u formuli.

za $\scriptstyle \Pi _{0}(x)$ imamo više složenu formulu

$\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.$

Ponovo, formula je validna za x > 1, dok  ρ su netrivijalne nule zeta funkcije prema njihovoj apsolutnoj vrijednosti, a, opet, drugi integralni, uzet sa minus znakom, je isto suma, ali tokom trivijalnih nula. Prvi termin li(x)je uobičajena logaritamska integralna funkcija; izraz li(x^ρ) u drugom terminu treba smatrati Ei(ρ ln x), gde Ei je analitički nastavak eksponencijalne integralne funkcije iz pozitivnih realnih brojeva u kompleksnoj ravni sa grane duž negativnih realnih brojeva.

Dakle Mebijusova inverzna funkcija nam daje

$\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

za x > 1, gde

$\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}$

je takozvana Rimanova R-funkcija. Poslednja serija koja je poznata je Gramova serija  i konvergira za sve pozitivn x.

Zbir svih netrivijalnih zeta nula u formuli za $\scriptstyle \pi _{0}(x)$ opisuje flustracije $\scriptstyle \pi _{0}(x)$, dok  preostali termini daju "uglađene" delove funkcije raspodele prostih brojeva, pa može se koristiti

$\operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

kao najbolji estimator $\scriptstyle \pi (x)$ za x > 1.

Amplituda "buke" je heuristički deo o $\scriptstyle {\sqrt {x}}/\ln x$, tako da fluktuacije raspodele prostih brojeva mogu biti jasno predstavljene sa Δ-funkcijom:

$\Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.$

Vrednosna tabela Δ(x) je dostupna.

Nejednakosti

Ovo su neke nejednakosti za π(x).

${\frac {x}{\ln x}}<\pi (x)<1.25506{\frac {x}{\ln x}}\!$za x ≥ 17.

Leva nejednakost prati za  x ≥ 17 i desna nejednakost prati za x > 1.  

Objašnjenje konstante 1.25506 dato je kao (sekvenca A209883 u OEIS)

Pjer Dursat je dokazao 2010 godine:

${\frac {x}{\ln x-1}}<\pi (x)$ za $x\geq 5393$, i

$\pi (x)<{\frac {x}{\ln x-1.1}}$ za $x\geq 60184$.

Ovo su neke nejednakosti za n-ti proste brojeve, p_n.

$n(\ln(n\ln n)-1)<p_{n}<n{\ln(n\ln n)}\!$ za n ≥ 6.

Leva nejednakost pokazuje za n ≥ 1 i desna nejednakost pokazuje za  n ≥ 6.

Aproksimacija za n-ti prost broj je

$p_{n}=n(\ln(n\ln n)-1)+{\frac {n(\ln \ln n-2)}{\ln n}}+O\left({\frac {n(\ln \ln n)^{2}}{(\ln n)^{2}}}\right).$

Rimanova hipoteza

Rimanova hipoteza je ekvivalntna mnogo čvršćim vezanim greškama u proceni za $\pi (x)$, i stoga je više ka redovnoj distribuciji prostih brojeva,

$\pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\log {x}).$

Vidi još

• Bertranov postulat
• Ojlerova pretpostavka
• Foias constant

Spoljašnje veze

• Chris Caldwell, The Nth Prime Page at The Prime Pages.
• Tomás Oliveira e Silva, Tables of prime-counting functions.