Дифузија

Дифузија представља спонтани транспорт материје или енергије под утицајем одговарајућег градијента из зоне више у зону ниже енергије или концентрације. Као и многи спонтани процеси, дифузија је ентропијски вођен процес у којем се енергија или материја која дифундује униформно распоређује у расположивом простору подижући тиме ентропију система.

Неке честице се растворе у чаши воде. У почетку су све честице близу једног горњег угла стакла. Ако се честице насумично крећу („дифузују“) у води, на крају постају распоређене насумично и равномерно из области високе концентрације у област ниске концентрације и организоване (дифузија се наставља, али без нето флукса).

Видео дифузије боје растворене у води у гел током дужег временског интервала.

Дифузија са микроскопске и макроскопске тачке гледишта. У почетку, постоје молекули раствора на левој страни баријере (љубичаста линија) и ниједан на десној. Баријера се уклања, а раствор се дифундује да би испунио цео контејнер. Врх: Један молекул се насумично креће. Средина: Са више молекула, постоји статистички тренд да растворена супстанца све уједначеније испуњава посуду. Доле: Са огромним бројем молекула растворене супстанце, сва случајност је нестала: изгледа да се растворена супстанца креће глатко и детерминистички из области високе концентрације у области ниске концентрације. Не постоји микроскопска сила која покреће молекуле удесно, али *изгледа* као да постоји на доњем панелу. Ова привидна сила се назива *ентропијска сила*.

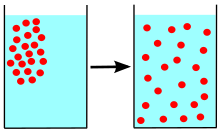
Сваки процес дифузије одвија се под утицајем одговарајућег градијента. Рецимо дифузија материје се одиграва под утицајем градијента концентрације а дифузија топлоте под утицајем градијента температуре. Дифузија је директна последица другог принципа термодинамике, који каже да ентропија неког неравнотежног система може само да расте, све док систем не дође у равнотежу. С обзиром да материја дифундује из области веће концентрације у област мање концентрације, систем прелази из уређенијег у мање уређен систем, тј. ентропија расте.

Фикови закони

Квантитативно, дифузија се описује Фиковим законима (први и други). Први Фиков закон каже да је флукс (Ј) пропорционалан градијенту концентрације. Други Фиков закон се изводи из једначине континуитета. У једнодимензионом систему:

Једначина континуитета:

{\frac {\partial c}{\partial t}}=-{\frac {\partial J}{\partial x}}

1. Фиков закон

J=-D{\frac {\partial c}{\partial x}}

2. Фиков закон

{\frac {\partial c}{\partial t}}={\frac {\partial }{\partial x}}\left(D{\frac {\partial c}{\partial x}}\right)

При чему за константан коефицијент дифузије, D, следи:

{\frac {\partial c}{\partial t}}=D{\frac {\partial ^{2}c}{\partial x^{2}}}

.

2. Фиков закон у тродимензионом систему

{\frac {\partial c}{\partial t}}=\nabla \cdot \left(D\nabla c\right)

Решавање дифузионе једначине је по правилу веома компликовано, тј. могуће само уз помоћ примене нумеричке математике.

Дифузија има изванредно важну улогу у свакодневном животу и у науци. У већини процеса у кухињи дифузија игра важну улогу од маринирања (дифузија зачина у намирницу) до кувања чаја (чај од слеза - остави се да из корена састојци будућег чаја дифундују у воду).

Дифузија је кључни процес у биолошким системима.

Дифузија наспрам запреминског протока

„Запремински проток“ је кретање/проток целог тела услед градијента притиска (на пример, вода која излази из славине). „Дифузија“ је постепено кретање/дисперзија концентрације унутар тела, услед градијента концентрације, без нето кретања материје. Пример процеса у коме се дешавају запреминско кретање и дифузија је људско дисање.^[1]

Прво, постоји процес „запреминског тока”. Плућа се налазе у грудној дупљи, која се шири као први корак у спољашњем дисању. Ово проширење доводи до повећања запремине алвеола у плућима, што узрокује смањење притиска у алвеолама. Ово ствара градијент притиска између ваздуха изван тела при релативно високом притиску и алвеола при релативно ниском притиску. Ваздух се креће низ градијент притиска кроз дисајне путеве плућа и улази у алвеоле све док притисак ваздуха и притисак у алвеолама не буду једнаки, то јест, кретање ваздуха масовним протоком престане када више не постоји градијент притиска.

Друго, постоји процес „дифузије”. Ваздух који стиже у алвеоле има већу концентрацију кисеоника од „устајалог” ваздуха у алвеолама. Повећање концентрације кисеоника ствара градијент концентрације кисеоника између ваздуха у алвеолама и крви у капиларама које окружују алвеоле. Кисеоник се затим креће дифузијом, низ градијент концентрације, у крв. Друга последица доласка ваздуха у алвеоле је смањење концентрације угљен-диоксида у алвеолама. Ово ствара градијент концентрације за дифузију угљен-диоксида из крви у алвеоле, пошто свеж ваздух има веома ниску концентрацију угљен-диоксида у поређењу са крвљу у телу.

Треће, постоји још један процес „запреминског тока“. Пумпно дејство срца затим транспортује крв по телу. Како се лева комора срца контрахује, запремина се смањује, што повећава притисак у комори. Ово ствара градијент притиска између срца и капилара, а крв се креће кроз крвне судове великим протоком низ градијент притиска.

Дифузија у контексту различитих дисциплина

Дифузионе пећи које се користе за термичку оксидацију

Концепт дифузије се широко користи у: физици (дифузија честица), хемији, биологији, социологији, економији и финансијама (дифузија људи, идеја и вредности цена). Међутим, у сваком случају супстанца или колекција која пролази кроз дифузију се „шири“ са тачке или локације на којој постоји већа концентрација те супстанце или колекције.

Постоје два начина да се уведе појам дифузије: феноменолошки приступ који почиње са Фиковим законима дифузије и њиховим математичким последицама, или физички и атомистички, разматрањем случајног хода честица дифузије.^[2]

У феноменолошком приступу, дифузија је кретање супстанце из области високе концентрације у област ниске концентрације без масовног кретања. Према Фиковим законима, дифузиони флукс је пропорционалан негативном градијенту концентрација. Она иде од региона веће концентрације ка регионима ниже концентрације. Нешто касније, различите генерализације Фикових закона су развијене у оквиру термодинамике и неравнотежне термодинамике.^[3]

Са атомистичке тачке гледишта, дифузија се сматра резултатом случајног хода честица које дифузују. У молекуларној дифузији, покретни молекули се сами покрећу топлотном енергијом. Насумично ходање малих честица у суспензији у течности открио је 1827. Роберт Браун, који је утврдио да та ситна честица суспендована у течном медију и довољно велика да буде видљива под оптичким микроскопом показује брзо и непрекидно неправилно кретање честица познато као Брауново кретање. Теорију Брауновог кретања и атомистичке позадине дифузије развио је Алберт Ајнштајн.^[4] Концепт дифузије се обично примењује на било коју тему која укључује насумичне шетње у групама појединаца.

У хемији и науци о материјалима, дифузија се односи на кретање молекула течности у порозним чврстим материјама.^[5] Молекуларна дифузија се одвија када је судар са другим молекулом вероватнији од судара са зидовима пора. У таквим условима, дифузивност је слична оној у неограниченом простору и пропорционална је средњем слободном путу. Кнудсенова дифузија, која се јавља када је пречник пора упоредив или мањи од средњег слободног пута молекула који дифундује кроз поре. Под овим условима, судар са зидовима пора постаје постепено вероватнији, а дифузност је нижа. Коначно, постоји конфигурациона дифузија, која се одвија ако молекули имају упоредиву величину са оном пора. Под овим условом, дифузивност је много нижа у поређењу са молекуларном дифузијом и мале разлике у кинетичком пречнику молекула узрокују велике разлике у дифузији.

Историја дифузије у физици

У временском оквиру, дифузија у чврстим телима је коришћена много пре него што је настала теорија дифузије. На пример, Плиније Старији је раније описао процес цементације, који производи челик од елемента гвожђа (Fe) путем дифузије угљеника. Други пример је добро познат вековима, дифузија боја витража или земљаног посуђа и кинеске керамике.

У савременој науци, прво систематско експериментално истраживање дифузије извео је Томас Грахам. Он је проучавао дифузију у гасовима, а главни феномен је описао 1831–1833:^[6]

„...гасови различите природе, када се доведу у контакт, не распоређују се према својој густини, најтежи доњи, а најлакши горњи, већ се спонтано, међусобно и равномерно, дифундују једни кроз друге и тако остају у интимном стању мешавине у било ком временском периоду."

Грахамова мерења су допринела да Џејмс Клерк Максвел 1867. изведе коефицијент дифузије за CO₂ у ваздуху. Стопа грешке је мања од 5%.

Године 1855, Адолф Фик, 26-годишњи демонстрант анатомије из Цириха, предложио је свој закон дифузије. Он је користио је Грахамово истраживање, наводећи свој циљ као „развој фундаменталног закона, за рад дифузије у једном елементу простора”. Он је утврдио дубоку аналогију између дифузије и провођења топлоте или електрицитета, стварајући формализам сличан Фуријеовом закону за провођење топлоте (1822) и Омовом закону за електричну струју (1827).

Роберт Бојл је демонстрирао дифузију у чврстим материјама у 17. веку^[7] продирањем цинка у бакарни новчић. Ипак, дифузија у чврстим телима није била систематски проучавана све до друге половине 19. века. Вилијам Чандлер Робертс-Остин, познати британски металург и бивши помоћник Томаса Грехама, проучавао је систематски дифузију чврстог стања на примеру злата у олову 1896. године:^[8]

„... Моја дуга веза са Грахамовим истраживањима учинила је то готово обавезом да покушам да проширим свој рад на течној дифузији на метале.“

Рудолф Клаузијус је 1858. увео концепт средњег слободног пута. Исте године Џејмс Клерк Максвел је развио прву атомистичку теорију транспортних процеса у гасовима. Модерну атомистичку теорију дифузије и Брауновог кретања развили су Алберт Ајнштајн, Маријан Смолуховски и Жан Батист Перен. Лудвиг Болцман је у развоју атомистичке позадине макроскопских транспортних процеса увео Болцманову једначину, која је математици и физици служила као извор идеја и брига о транспортним процесима више од 140 година.^[9]

У периоду 1920–1921, Џорџ де Хевеси мерио је самодифузију коришћењем радиоизотопа. Проучавао је самодифузију радиоактивних изотопа олова у течном и чврстом олову.

Јаков Френкел (понекад, Јакоб Френкел) је предложио и разрадио 1926. идеју о дифузији у кристалима кроз локалне дефекте (празнине и међупросторне атоме). Он је закључио да је процес дифузије у кондензованој материји ансамбл елементарних скокова и квазихемијских интеракција честица и дефеката. Он је увео неколико механизама дифузије и пронашао константе брзине из експерименталних података.

Нешто касније, Карл Вагнер и Волтер Х. Шотки су даље развили Френкелове идеје о механизмима дифузије. Тренутно је универзално признато да су атомски дефекти неопходни за посредовање дифузије у кристалима.^[8]

Хенри Ејринг је, са коауторима, применио своју теорију апсолутних брзина реакција на Френкелов квазихемијски модел дифузије.^[10] Аналогија између кинетике реакције и дифузије доводи до различитих нелинеарних верзија Фиковог закона.^[11]

Види још

Дифузија кроз ћелијску мембрану

Референце

^ Muir, D. C. F. (1966-10-01). „Bulk flow and diffusion in the airways of the lung”. British Journal of Diseases of the Chest (на језику: енглески). 60 (4): 169—176. ISSN 0007-0971. PMID 5969933. doi:10.1016/S0007-0971(66)80044-X.
^ J. Philibert (2005). One and a half century of diffusion: Fick, Einstein, before and beyond. Архивирано 2013-12-13 на сајту Wayback Machine Diffusion Fundamentals, 2, 1.1–1.10.
^ S.R. De Groot, P. Mazur (1962). Non-equilibrium Thermodynamics. North-Holland, Amsterdam.
^ A. Einstein (1905). „Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen”. Ann. Phys. 17 (8): 549—60. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806  .
^ Pescarmona, P.P. (2020). Gitis, V.; Rothenberg, G, ур. Handbook of Porous Materials (на језику: енглески). 4. Singapore: WORLD SCIENTIFIC. стр. 150—151. ISBN 978-981-12-2328-0. doi:10.1142/11909.
^ Diffusion Processes, Thomas Graham Symposium, ed. J.N. Sherwood, A.V. Chadwick, W.M.Muir, F.L. Swinton, Gordon and Breach, London, 1971.
^ L.W. Barr (1997), In: Diffusion in Materials, DIMAT 96, ed. H.Mehrer, Chr. Herzig, N.A. Stolwijk, H. Bracht, Scitec Publications, Vol.1, pp. 1–9.
^ ^а ^б H. Mehrer; N.A. Stolwijk (2009). „Heroes and Highlights in the History of Diffusion” (PDF). Diffusion Fundamentals. 11 (1): 1—32.
^ S. Chapman, T. G. Cowling (1970) The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, Cambridge University Press (3rd edition), ISBN 052140844X.
^ J.F. Kincaid; H. Eyring; A.E. Stearn (1941). „The theory of absolute reaction rates and its application to viscosity and diffusion in the liquid State”. Chem. Rev. 28 (2): 301—65. doi:10.1021/cr60090a005.
^ A.N. Gorban, H.P. Sargsyan and H.A. Wahab (2011). „Quasichemical Models of Multicomponent Nonlinear Diffusion”. Mathematical Modelling of Natural Phenomena. 6 (5): 184—262. S2CID 18961678. arXiv:1012.2908  . doi:10.1051/mmnp/20116509  .

Спољашње везе

[1] Muir, D. C. F. (1966-10-01). „Bulk flow and diffusion in the airways of the lung”. British Journal of Diseases of the Chest (на језику: енглески). 60 (4): 169—176. ISSN 0007-0971. PMID 5969933. doi:10.1016/S0007-0971(66)80044-X.

[2] J. Philibert (2005). One and a half century of diffusion: Fick, Einstein, before and beyond. Архивирано 2013-12-13 на сајту Wayback Machine Diffusion Fundamentals, 2, 1.1–1.10.

[3] S.R. De Groot, P. Mazur (1962). Non-equilibrium Thermodynamics. North-Holland, Amsterdam.

[4] A. Einstein (1905). „Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen”. Ann. Phys. 17 (8): 549—60. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806  .

[5] Pescarmona, P.P. (2020). Gitis, V.; Rothenberg, G, ур. Handbook of Porous Materials (на језику: енглески). 4. Singapore: WORLD SCIENTIFIC. стр. 150—151. ISBN 978-981-12-2328-0. doi:10.1142/11909.

[6] Diffusion Processes, Thomas Graham Symposium, ed. J.N. Sherwood, A.V. Chadwick, W.M.Muir, F.L. Swinton, Gordon and Breach, London, 1971.

[7] L.W. Barr (1997), In: Diffusion in Materials, DIMAT 96, ed. H.Mehrer, Chr. Herzig, N.A. Stolwijk, H. Bracht, Scitec Publications, Vol.1, pp. 1–9.

[Mehrer2009-8] а ^б H. Mehrer; N.A. Stolwijk (2009). „Heroes and Highlights in the History of Diffusion” (PDF). Diffusion Fundamentals. 11 (1): 1—32.

[ChapmanCowling-9] S. Chapman, T. G. Cowling (1970) The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, Cambridge University Press (3rd edition), ISBN 052140844X.

[10] J.F. Kincaid; H. Eyring; A.E. Stearn (1941). „The theory of absolute reaction rates and its application to viscosity and diffusion in the liquid State”. Chem. Rev. 28 (2): 301—65. doi:10.1021/cr60090a005.

[GorbanMMNP2011-11] A.N. Gorban, H.P. Sargsyan and H.A. Wahab (2011). „Quasichemical Models of Multicomponent Nonlinear Diffusion”. Mathematical Modelling of Natural Phenomena. 6 (5): 184—262. S2CID 18961678. arXiv:1012.2908  . doi:10.1051/mmnp/20116509  .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]