Лагранжова теорема

Уколико сте тражили теорему из теорије група, погледајте чланак Лагранжова теорема (теорија група).

Лагранжова теорема (енгл. mean value theorem) је једна од основних теорема диференцијалног рачуна и уопште математичке анализе. Често се још назива и теорема о средњој вредности диференцијалног рачуна.

Геометријска интерпретација Лагранжове теореме

Формулација

Ако је функција f:

• непрекидна на затвореном интервалу $\,[a,b]$, и
• диференцијабилна на отвореном интервалу $\,(a,b)$,

онда постоји тачка $\,c$ из интервала $\,(a,b)$, таква да је:

${\frac {f(b)-f(a)}{b-a}}=f'(c)$

Доказ 1

Посматрајмо функцију

$h(x)=f(x)+\lambda x$.

И она је непрекидна на $\,[a,b]$ и диференцијабилна на $\,(a,b)$. Одредимо $\lambda$ за које функција $\,h(x)$ задовољава услове Ролове теореме.

Дакле, да би било $\,h(a)=h(b)$, мора бити:

$\lambda =-{\frac {f(b)-f(a)}{b-a}}.$

Тада, по условима Ролове теореме, постоји тачка $\,c$ из интервала $\,(a,b)$, таква да је:

$0=h'(c)=f'(c)+\lambda ,$ те је

$f'(c)={\frac {f(b)-f(a)}{b-a}}.$

Доказ 2

Посматрајмо функцију

$h(x)=f(x)-f(a)-({\frac {f(b)-f(a)}{b-a}})(x-a)$

Како је функција $f$ непрекидна и диференцијаблна на интервалу $[a,b]$, односно $(a,b)$, и функција $h$ је непрекидна и диференцијабилна на истим интервалима. Шта више, $h(a)=h(b)=0$, што значи да на функцију $h$ можемо применити Ролову теорему.

Први извод функције $h$ је:

$h'(x)=f'(x)-{\frac {f(b)-f(a)}{b-a}}$

Према Роловој теореми сада следи да постоји тачка $c$, таква да је $f'(c)=0$, тј.

$0=h'(c)=f'(c)-{\frac {f(b)-f(a)}{b-a}}$,

односно:

$f'(c)={\frac {f(b)-f(a)}{b-a}}$,

што је и требало да се покаже.

Геометријска интерпретација

Геометријска интерпретација: За било коју функцију непрекидну на [a, b] и диференцијабилну на (a, b), постоји тачка c из интервала (a, b) у којој је тангента (tangent) паралелна са сечицом (secant) која повезује крајеве интервала [a, b].

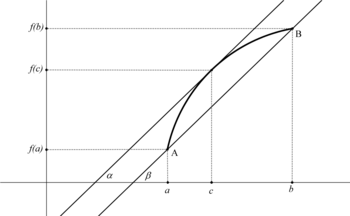
Геометријски значај ове теореме се састоји у томе да под датим условима постоји тангента криве $\,y=f(x)$ у некој тачки $\,c$, која припада затвореном интервалу $\,(a,b)$, паралелна са сечицом која пролази кроз тачке $\,A=(a,f(a))$ и $\,B=(b,f(b)).$

Механичка интерпретација

Ако се тачка креће по закону $\,x=x(t)$, где је $x(t)$ непрекидна на $[a,b]$ и диференцијаблна на $(a,b)$, онда постоји тренутак $\,t_{0}$ у ком је тренутна брзина $x'(t_{0})$ једнака средњој брзини на интервалу $[a,b]$, која износи $\,{\frac {f(b)-f(a)}{b-a}}$, управо јер постоји то $\,t_{0}$ када је: $\,f'(t_{0})={\frac {f(b)-f(a)}{b-a}}.$

Последице и напомене

• Као ни Ролова теорема, ни Лагранжова теорема нам не даје информацију о конструкцији тачке $\,c$, као ни о броју таквих тачака.
• Такође, последица Лагранжове теореме је и следеће: Ако је за свако $\,x$ из затвореног интервала $\,[a,b]$, $\,f'(x)=0$, онда је функција $\,f$ константна на затвореном интервалу $\,[a,b]$.
• Лагранжова теорема се може посматрати као уопштење Ролове теореме. Наиме, за $\,f(a)=f(b)$, добијамо функцију која испуњава све услове Ролове теореме.
• Два важна уопштења Лагранжове формуле, тј. теореме, су Кошијева теорема и Тејлорова теорема.

Види још

• Кошијева теорема
• Тејлорова теорема
• Ролова теорема
• Теореме средње вредности
• Интервал
• Математичка анализа