Википедија

Direktan aciklični graf

директан граф без усмерених циклуса

Direktan aciklični graf (DAG) u matematici i informatici je direktan graf bez usmerenih ciklusa. Sastoji se od zbira čvorova i usmerenih grana, svaka grana povezuje jedan čvor sa drugim, tako da ne postoji način da se počne u nekom čvoru v i prati redosled grana koji se na kraju petlje opet vraća na čvor v. [1][2][3]

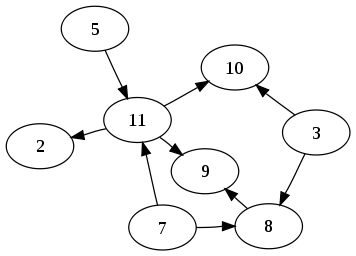
Primer direktnog acikličnog grafa

DAG može da se koristi za modeliranje mnogih različitih vrsta informacija. Dostizanje veze u DAG formi delimičnog reda, i bilo kog konačno delimičnog reda može biti predstavljen od strane DAG koji koristi dostizanje. Kolekcija zadataka koja se mora odrediti u nizu, uz ograničenje da moraju biti izvršeni određeni zadaci ranije od drugih, može biti predstavljen kao DAG sa čvorom za svaki zadatak i granom za svaku prepreku; algoritmi za topološko uređenje mogu se koristiti za određivanje ispravnog niza. Dodatno, DAG može da se koristi kao prostor efikasne zastupljenosti nizova sa preklapajućim podnizovima. DAG se takođe koristi za predstavljanje sistema događaja ili potencijalnih događaja i uzročno–posledičih odnosa između njih. DAG se takođe može koristiti za modelovanje procesa u kojima je protok podataka u doslednom pravcu kroz mrežu procesora, ili stanja repozitorijuma u verziji kontole sistema.

Odgovarajući koncept neusmerenih grafova je šuma, jedan neusmeren graf bez ciklusa. Izbor orijentacije za šume proizvodi posebnu vrstu direktnog acikličnog grafa koji se zove orijentisano stablo. Međutim, postoje mnoge druge vrste direktnog acikličnog grafa koje nisu formirane prem orijentaciji grana jednog neusmerenog acikličnog grafa. Osim toga, svaki neusmereni graf ima acikličnu orijentaciju, dodelu pravca za svoje grane koje ga čine direktnim acikličnim grafom. Iz tih razloga bilo bi preciznije nazvati direktan aciklični graf acikličan usmereni graf ili acikličan digraf.

Matematička svojstva uredi

Dostizanje, tranzitivno zatvorenje, i tranzitivna redukcija uredi

 
Haseov dijagram koji predstavlja parcijalan red ⊆ između podskupova od tri elementa skupa.

Svaki usmereni aciklični graf dovodi do parcijalnog reda ≤ na svojim čvorovima, gde je u ≤ v tačno kada postoji direktan put od u do v u DAG.[4] Međutim, mnogo različitih DAG može dovesti do tog istog dostižnosti odnosa: [5] na primer, DAG sa dve grane a → b i b → c ima isto dostizanje kao i graf sa tri grane a → b, b → c, i a → c. Ako je G DAG, njegova tranzitivna redukcija je graf sa najmanjim brojem grana koji predstavlja isto dostizanje kao i za G, a njegovo tranzitivno zatvorenje je graf sa najviše grana koji predstavlja isto dostizanje. Tranzitivna redukcija i tranzitivno zatvorenje su jedinstveno definisani za DAG; nasuprot tome, za usmereni graf koji nije acikličan, ne može biti više od jednog minimlnog podgrafa sa istim dostizanjem odnosa. [6]

Tranzitivno zatvaranje na G ima jednu granu u → v za svaki vezani par u ≤ v različitih elemenata u dostizanju odnosa G, i tako se može posmatrati kao direktan prevod dostizanja odnosa ≤ u graf - teorijskom smislu: svaki parcijalni red skupa može se prevesti u DAG na ovaj način. Ako DAG G predstavlja parcijalni red ≤, onda je tranzitivna redukcija od G podgraf od G sa jednom granom u → v za svaki par u propratnom odnosu ≤; tranzitivne redukcije su korisne u vizualizaciji parcijalnih redova koje oni predstavljaju, jer imaju manje grana od drugih grafova koji predstavljaju iste redove i samim tim dovode do jednostavnijih crteža grafova. Hase dijagram parcijalnog red je crtež tranzitivne redukcije u kojima je orijentacija svake grane prikazana tako da je početni čvor grane na nižem nivou nego njegov krajnji čvor. [7]

Topološko sortiranje uredi

Svaki direktan aciklični graf ima topološko sortiranje, tj. redosled čvorova je takav da se početak krajnje tačke svake grane javlja ranije u sortiranju od kraja krajnje tačke grane. U principu, ovo sortiranje nije jedinstveno; DAG ima jedinstveno topološko sortiranje ako i samo ako ima usmeren put koji sadrži sve vrhove, u kom slučaju sortiranje je isto kao i red u kojem se čvorovi pojavljuju na putu. [8] Porodica topološkog sortiranja jednog DAG je ista kao i porodica linearnih produžetaka dostižnosti u odnosu na DAG, [9], tako bilo koja dva grafa predstavljaju isti prcijalni red sa istim skupom topoloških redova.

Kombinatorno nabrajanje uredi

Problem grafa nabrajanja brojanja direktnog acikličnog grafa ispitivao je Robinson (1973). [10] Broj DAG sa n obeleženih čvorova, za n = 0, 1, 2, 3,....,(dozvoljavajući da se ovi brojevi pojave u bilo kom redu u topološkom sortiranju DAG) je

1, 1, 3, 25, 543, 29281, 3781503, … (red A003024 u OEIS).

Ovi brojevi se mogu izračunati ponavljanjem veze:

 [10]

Erik V. Veinstejn je pretpostavio, [11] a McKay et al. 2004 dokazao, [12] da isti brojevi broje (0,1) matrice u kojoj su sve svojestvene vrednosti pozitivni realni brojevi. Dokaz je bijekcija: Matrica A je matrica povezanosti DAG ako i samo ako je A + I (0,1) matrica sa svim svojstveno pozitivnim vrednostima, gde I označava matricu identiteta. Zato što DAG ne može imati ciklus, njegova susedna matrica mora imati nula dijagonalu, dodajući I da sačuva osobine da su sve matrice koeficijenta 0 ili 1.

Veza porodice grafa uredi

Orijentisano stablo je usmereni graf formiran prema orijetaciji grana slobodnog stabla.[13] Svako orijentisano stablo je DAG. Konkretno, istina je da su stabla formirana na osnovu usmerenja svih grana od spolja ka korenu stabla. Snažno nedvosmislen graf predstavlja usmereni graf u kojem postoji najviše jedna usmerena putanja (u oba smera) između bilo koja dva čvora; eventualno, to je DAG u kojem, za svaki čvor v, postoji skup čvorova dostupnih iz v oblikovnog stabla. [14]

Računarski problemi uredi

Topološko sortiranje i prepoznavanje uredi

Glavni članak: Topološko sortiranje

Topološko sortiranje je algoritam problema pronalaženja topološkog sortiranja; može se rešiti u linearnom vremenu. [15] Kanov algoritam za topološko sortiranje gradi čvorove direktnog sortiranja, održavajući listu čvorova koji nemaju grane, povezujući ih sa čvorovima koji nisu već navedeni, a više puta dodajući jedan takav čvor na kraj liste koja se osniva.[16] Alternativno, topološko sortiranje se može konstruisati unazad posle sortiranja numeracije od prve pretrage u dubinu grafa.[15]

Takođe je moguće da se proveri da li je dati usmereni graf DAG u linearnom vremenu ili je bilo pokušaja da nađe topološko sortiranje a zatim testiranje za svaku granu da li je različito sortiranje ispravno [17] ili alternativno, za neke algoritme topološkog sortiranja, proverava se da li algoritam uspešno sortira sve čvorove bez greške.[16]

Građa cikličnih grafova uredi

Svaki neusmereni graf može biti u DAG izborom ukupnog sortiranja svojih čvorova i orijentacije svojih grana iz ranije krajnje tačke u sortirane kasnije krajnje tačke. Međutim, različita potpuna sortiranja mogu dovesti do iste aciklične orijentacije. Broj acikličnih orijentacija je jednak |χ(−1)|, gde je χ hromatski polinom datog grafa. [18]

Bilo koji usmereni graf se može predstaviti kao DAG tako što se ukloni skup povratnih čvorova ili skupa povratnih lukova. Međutim, najmanji takav skup je NP-teški problemi.[19] Proizvoljno usmeren graf može da se transformiše u DAG, naziva se kondenzacija, ugovaranjem svake od njegovih čvrsto povezanih komponenti u jedan superčvor. [20] Kada je graf već acikličan njegov najmanji skup povratnih informacija čvorova i skup povratnih informacija lukova su prazni, a njegova kondenzacija je sam graf.

Tranzitivno zatvorenje i tranzitivna redukcija uredi

Tranzitivno zatvorenje datog DAG, sa n čvorova i m grana, može se konstruisati u vremenu O(mn) koristeći ili pretragu u širinu ili pretragu u dubinu radi testiranja dostizanja do svakog čvora. [21] Alternativno, može se rešiti i u vremenu O(nω) gde je ω < 2.373 eksponent za brzo množenje algoritama matrice; ovo je teoretski napredak u odnosu na O(mn) vezan za guste grafove. [22]

U svim ovim algoritmima tranzitivnog zatvorenja, moguće je razlikovati parove čvorova koji su dostupni najmanje jedne putanje dužine dva ili više od parova koji se mogu povezati samo od dužine jedne putanje. Tranzitivna redukcija sastoji se od grana čije su dužine jedne putanje jedine putanje koje povezuju svoje krajnje tačke. Stoga, tranzitivna redukcija se može konstruisati u istom asimptotskom vremenu graničnih linija kao i tranzitivna zatvorenost. [23]

Problem zatvorenja uredi

Glavni članak: Problem zatvorenja

Problem zatvorenja uzima kao ulaz direktan aciklični graf sa težinama njenih čvorova i traži minimalnu (ili maksimalnu) težinu zatvaranja, skup čvorova bez ikakvih odlazećih grana. (Problem može biti formulisan za usmerene grafove bez pretpostavke da su acikliči, ali bez veće uopštenosti jer u ovom slučaju je ekvivalean sa problemom kondenzacije grafova.) Može se rešiti u polinomijalnom vermenu koristeći smanjen maksimalan problem toka.[24]

Aplikacije uredi

Algoritam putanje uredi

Neki algoritmi postaju jednostavniji kada se koristi DAG umesto opštih grafova, na osnovu principa topološkog sortiranja. Na primer, moguće je naći najkraće puteve i najduže puteve sa datim početnim čvorom u DAG u linearnom vremenu obradom čvorova u topološkom redu, i izračunavanje dužine puta za svaki čvor da bude minimalna ili maksimalna dužina dobijena preko prethodnih grana. [25] Nasuprot tome, za proizvoljne grafove najkraći put može zahtevati sporiji algoritam kao što je Dajkstrin algoritam ili Belman-Fordov algoritam, [26] i najduži put u proizvoljnom grafu je NP-teški problemi.[27]

Raspoređivanje uredi

DAG reprezentacije parcijalnog sortiranja ima mnogo zahteva u rasporedu problema za sisteme zadataka sa ograničenim sortiranjem. [28] Na primer, DAG može koristiti tabelu za opisivanje zavisnosti između ćelija: ako se jedna ćelija izračunava po formuli koja uključuje vrednost druge ćelije, nacrtati DAG granu od druge ćelije do prve. Ako se ulazne vrednosti tabele promene, sve preostale vrednosti tabele mogu se preračunati sa jednom promenom po ćeliji, od topološkog sortiranja ćelija i ponovo vrednuje svaku ćeliju u tom cilju.[29] Slični problemi zadatka sortiranja nastaje u pravljenju fajlova za kompilaciju programa,[29] uputstvo za raspored za nizak nivo optimizacije računarskog programa, [30] i Pert raspored za upravljanje velikih ljudskih projekata. [31] Grafik zavisnosti bez kružne zavisnosti oblika direktnog acikličnog grafa.

Obrada podataka mreže uredi

Usmeren graf može da se koristi za predstavljanje mreže za obradu elemenata; u ovoj formulaciji podaci, ulazni podaci obrađuju element preko prethodnih grana i napuštaju element preko odlazećih grana. Primeri ovoga obuhvataju sledeće:

  • U dizajnu elektronskih kola, statički kombinacioni logički blokovi mogu biti predstavljeni kao aciklični sistemi logičkih kola koji izračunava funkciju jednog ulaza, gde su ulaz i izlaz funkcije predstavljeni kao pojedinačni bit. U principu, izlaz ovih blokova ne može da se koristi kao ulaz osim ako je zauzet od strane registra ili glavnog elementa koji održava svoja aciklična svojstva. [32] Šema elektronskog kružnog puta ili na papiru ili u bazi podataka je oblik direktnog acikličnog grafa koji koristi objekte ili komponente za formiranje usmerene reference na nižem nivou komponente. Sama elektronska kola nisu nužno aciklična ili usmerena.
  • Protok podataka programski jezici opisuju sisteme vrednosti koji se odnose na međusobno direktan aciklični graf. Kada promene jednu vrednost, njegovi naslednici se preračunavaju; svaka vrednost je procenjena kao funkcija svojih prethodnika u DAG. [33]
  • U kompajleru, ravna linija koda (koji je, sekvenca iskaza bez petlje ili uslovna grana) može biti predstavljen DAG koji opisuje ulaze i izlaze svake aritmetičke operacije koja se obavlja u kodu; ovo predstavljanje omogućava da kompajler obavlja zajedničko eliminisanje podizraz efikasno.[34]
  • U većini sistema za tabele, grafikon zavisnosti povezuje jednu ćeliju sa drugom ukoliko prva ćelija čuva formulu koja koristi vrednost druge ćelije tako da mora biti direktan aciklični graf. Ciklusi zavisnosti su poništeni jer oni uzrokuju ćelije uključene u ciklus koji nema dobro definisanu vrednost. Pored toga, zahteva se da zavisnost bude aciklična i omogućava topološko sortiranje koje se koristi da zakaže ponovni preračun vrednosti ćelija kada se menja tabela.[29]

Uzročne strukture uredi

Grafovi koji imaju čvorove koji predstavljaju događaje, i grane koje predstavljaju uzročno-veze između događaja, često su aciklični [35] - uređenje čvorova u linearnom rasporedu vremena, sve strelice ukazuju u istom pravcu kao vreme, od roditelja na dete (zbog uzročnosti utiče budućnost a ne prošlost), i na taj način nemaju petlje.

Na primer, Bajesova mreža predstavlja sistem verovatnoće događaja kao čvorova u direktnom acikličnom grafu, u kojoj se verovatoća nekog događaja može izračunati iz verovatnoće svojih prethodnika u DAG. [36] U tom kontekstu, moralni graf DAG je neusmereni graf stvoren dodavanjem (neusmerenih) grana između svih roditelja istog čvora (ponekad zovemo brak), a zatim zamenite sve usmerene grane sa neusmerenim granama. [37]

Drugi tip grafa sa sličnom uzročnom strukturom ima uticaj dijagrama, čvorovi na kojima su predstavljene odluke da budu ili nepoznate informacije, kao i grane koje predstavljaju uzročne uticaje iz jednog čvora na drugi. [38] U epidemiologiji, na primer, ovi dijagrami se često koriste za procenu očekivane vrednsoti različitih izbora za intervenciju. [39][40] Uloga DAG u ovim aplikacijama je da ga pretvori iu uzročne-posledične pretpostavke u uslovno nezavisna ograničenja, što se može pročitati iz DAG koristeći Pearl d-separaciju. [41] i testiran u podacima.

Genealogija i istorijska verzija uredi

Porodica stabala se takođe može posmatrati kao direktan aciklični graf, sa lvorom za svakog člana porodice i grane za svaku vezu roditelj-dete.[42] Uprkos imenu, ti grafovi nisu nužno stabla zbog mogućnosti brakova između rođaka (tako da dete ima zajedničkog pretka na obe strane majke i oca) izazivajući pedigre kolapsa. (Grafovi po majčinoj liniji porekla ("majka" odnosi između žena) i po očevoj liniji porekla ("otac" odnosi između muškaraca) su stabla u okviru ovog grafa.) Zato što niko ne može postati samostalno predak, ovi grafoi su ciklilni.

Iz istog razloga, istorijska verzija distribuiranog upravljačkog sistema revizije uglavnom ima strukturu direktnog acikličnog grafa, u kojima postoji čvor za svaku reviziju i grane povezuju parove revizije koje su direktno izvedene od drugog; ovo nisu stabla u celini zbog stapanja. [43]

U mnogim slučajnim algoritmima u računarskoj geometriji, algoritam održava istoriju DAG predstavlja istorijsku verziju geometrijske strukture tokom perioda niza promena u strukturi. Na primer, u slučajnom pojedinačnom algoritmu za Delunai triangulacija, triangulacija promene zamenom jednog trougla sa tri manja trougla kada svaka tačka doda, i "flip" operacija zamenjuje parove trouglova. Istorija DAG za ovaj algoritam ima čvorove za svaki trougao izgrađen kao deo algoritma, i grane svakog trougla, dva ilo tri trougla koji ga zamnenjuju. Traženje puta kroz ovaj DAG predstavlja niz trouglova koji sadrže pojedinačnu tačku koja omogućava tačku lokacije puta koja će biti efikasno odgovorio. [44]

Sažimanje podataka uredi

Druga vrsta primene direktnog acikličnog grafa nastaje u sažetom predstavljanju niza sekvenci kao putanja u grafu. Na primer, usmereni aciklički graf reči je struktura podataka u kompjuterskoj nauci formiran od strane direktnog acikličnog grafa sa jednim izvorom i sa granama označenim slovima ili simbolima; putevi od izvora do ponora u ovom grafu predstavljaju skup niski, kao što su Engleske reči. [45] Bilo koji niz sekvenci se može predstaviti kao put u stablu, formiranjem čvora stabla za svaki prefiks sekvenci i izgrađivanjem roditelja jednog od tih čvorova koji predstavljaju sekvencu sa jednim manje elementom; stablo formirano na ovaj način sa nizom niski zove se trie. Usmeren aciklični graf reči štedi prostor nad trie dozvoljavajući da se putevi razilte i ponovo pridružuju, tako da se skup reči sa istim mogućim nastavcima mogu biti predstavljeni jednim čvorom stabla.

Ista ideja koristeći DAG predstavlja porodicu putanja javlja se u binarnom dijagramu odluke, [46][47] DAG - zasnovan na strukturi i podacima za predstavljanje binarnih funkcija. U binarnom dijagramu odluke, svaki ne-potonuli čvor obeležen imenom binarne promenljive, a svaki potonuli i svaka grana je obeležena 0 ili 1. Funkcija vrednosti za bilo koji istiniti zadatak promenljive je vrednost u potonulom traženju sledećeg puta, počevši od jednog izvora čvora, da na svakom ne-potonulom čvoru prati odlaznu granu označenu sa vrednošću čvora promenljive. Baš kao što se usmereni aciklični graf reči može posmatrati kao komplikovani oblik pokušaja, binarna odluka dijagrama se može posmatrati kao komplikovan oblik stabla odlučivanja koja štedi prostor tako što putanje dozvoljavaju da se ponovo dogovore o rezultatima svih preostalih odluka.

Reference uredi

  1. ^ Christofides, Nicos . Graph theory: an algorithmic approach. . Academic Press. 1975. pp. 170–174. 
  2. ^ Thulasiraman, K.; Swamy, M. N. S. . "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms, John Wiley and Son. 1992. ISBN 978-0-471-51356-8. str. 118.
  3. ^ Bang-Jensen, Jørgen. "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag. 2008. ISBN 978-1-84800-997-4. str. 32–34.
  4. ^ Kozen, Dexter . The Design and Analysis of Algorithms, Monographs in Computer Science. . Springer. 1992. ISBN 978-0-387-97687-7. 
  5. ^ Banerjee, Utpal . "Exercise 2(c)", Loop Transformations for Restructuring Compilers: The Foundations. . Springer. 1993. pp. 19. ISBN 978-0-7923-9318-4. 
  6. ^ Bang-Jensen, Jørgen; Gutin, Gregory Z. . "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics. . Springer. 2008. pp. 36–39. ISBN 978-1-84800-998-1. 
  7. ^ Jungnickel, Dieter . Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics 5. . Springer. 2012. pp. 92–93. ISBN 978-3-642-32278-5. 
  8. ^ Sedgewick, Robert; Wayne, Kevin , "4,2,25 Unique topological ordering", Algorithms (4th ed.). . Addison-Wesley. 2011. pp. 598–599. ISBN 978-0-13-276256-4. 
  9. ^ Bender, Edward A.; Williamson, S. Gill , "Example 26 (Linear extensions – topological sorts)", A Short Course in Discrete Mathematics, Dover Books on Computer Science. . Courier Dover Publications. 2005. pp. 142. ISBN 978-0-486-43946-4. 
  10. ^ a b Robinson, R. W. (1973), „Counting labeled acyclic digraphs”, Ur.: Harary, F., New Directions in the Theory of Graphs, Academic Press, str. 239—273 . See also Harary, Frank; Palmer, Edgar M. (1973), Graphical Enumeration, Academic Press, str. 19, ISBN 978-0-12-324245-7 
  11. ^ Weisstein, Eric W., "Weisstein's Conjecture", MathWorld.
  12. ^ McKay, B. D.; Royle, G. F.; Wanless, I. M.; Oggier, F. E.; Sloane, N. J. A.; Wilf, H. (2004), "Acyclic digraphs and eigenvalues of (0,1)-matrices", Journal of Integer Sequences 7, Article 04.3.3.
  13. ^ Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987 (PDF). str. 222–228.
  14. ^ Furnas, George W.; Zacks, Jeff (1994). „Multitrees: enriching and reusing hierarchical structure”. Proceedings of the SIGCHI conference on Human factors in computing systems celebrating interdependence - CHI '94. str. 330—336. ISBN 0897916506. S2CID 18710118. doi:10.1145/191666.191778. 
  15. ^ a b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. Introduction to Algorithms (2nd izd.). MIT Press and McGraw-Hill. ISBN 0-262-03293-7.  Section 22.4, Topological sort. str. 549–552.
  16. ^ a b Jungnickel 2012, str. 50–51
  17. ^ For depth-first search based topological sorting algorithm, this validity check can be interleaved with the topological sorting algorithm itself; see e.g. Skiena, Steven S. , The Algorithm Design Manual. . Springer. 2009. pp. 179–181. ISBN 978-1-84800-070-4. 
  18. ^ Stanley, Richard P. (1973). „Acyclic orientations of graphs”. Discrete Mathematics. 5 (2): 171—178. doi:10.1016/0012-365X(73)90108-8. 
  19. ^ Garey, Michael R.; Johnson, David S. , Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman. 1979. ISBN 978-0-7167-1045-5. Problems GT7 and GT8. str. 191–192.
  20. ^ Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, John Wiley & Sons. str. 63.
  21. ^ Skiena 2009, str. 495.
  22. ^ Skiena 2009, str. 496.
  23. ^ Bang-Jensen & Gutin (2008). str. 38.
  24. ^ Picard, Jean-Claude (1976). „Maximal Closure of a Graph and Applications to Combinatorial Problems”. Management Science. 22 (11): 1268—1272. doi:10.1287/mnsc.22.11.1268. 
  25. ^ Cormen 2001, str. 592–595.
  26. ^ Cormen et al. 2001, Sections 24.1, The Bellman–Ford algorithm. str. 588–592, and 24.3, Dijkstra's algorithm. str. 595–601.
  27. ^ Cormen 2001, str. 966.
  28. ^ Skiena 2009, str. 469.
  29. ^ a b v Gross, Yellen & Zhang 2013, str. 1181
  30. ^ Srikant, Y. N.; Shankar, Priti . The Compiler Design Handbook: Optimizations and Machine Code Generation, (2nd ed.). . CRC Press. 2007. pp. 19–39. ISBN 978-1-4200-4383-9. 
  31. ^ Wang, John X. . What Every Engineer Should Know About Decision Making Under Uncertainty. . CRC Press. 2002. pp. 160. ISBN 978-0-8247-4373-4. 
  32. ^ Sapatnekar, Sachin , Timing. . Springer. 2004. pp. 133. ISBN 978-1-4020-7671-8. 
  33. ^ Programming Symposium. Lecture Notes in Computer Science. 19. 1974. ISBN 978-3-540-06859-4. S2CID 38955165. doi:10.1007/3-540-06859-7. 
  34. ^ Touati & de Dinechin 2014, str. 123
  35. ^ Gopnik, Alison; Schulz, Laura . Causal Learning. . Oxford University Press. 2007. pp. 4. ISBN 978-0-19-803928-0. 
  36. ^ Shmulevich, Ilya; Dougherty, Edward R. , Probabilistic Boolean Networks: The Modeling and Control of Gene Regulatory Networks, Society for Industrial and Applied Mathematics. 2010. ISBN 978-0-89871-692-4. str. 58.
  37. ^ Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. , "3.2.1 Moralization", Probabilistic Networks and Expert Systems. . Springer. 1999. pp. 31–33. ISBN 978-0-387-98767-5. 
  38. ^ Dorf, Richard C. . The Technology Management Handbook. . CRC Press. 1998. pp. 9–7. ISBN 978-0-8493-8577-3. 
  39. ^ Boslaugh, Sarah , Encyclopedia of Epidemiology, Volume 1, SAGE. 2008. ISBN 978-1-4129-2816-8. str. 255.
  40. ^ Pearl, Judea (1995). „Causal diagrams for empirical research”. Biometrika. 82 (4): 669—688. doi:10.1093/biomet/82.4.669. 
  41. ^ Bayesian network
  42. ^ Kirkpatrick, B. B. (2011). „Haplotypes versus genotypes on pedigrees”. Algorithms for Molecular Biology : Amb. 6 (1): 10. PMC 3102622  . PMID 21504603. doi:10.1186/1748-7188-6-10. 
  43. ^ Bartlang, Udo , Architecture and Methods for Flexible Content Management in Peer-to-Peer Systems. . Springer. 2010. pp. 59. ISBN 978-3-8348-9645-2. 
  44. ^ Pach, János; Sharir, Micha, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical surveys and monographs 152, American Mathematical Society. ISBN 978-0-8218-7533-9. str. 93–94.
  45. ^ Combinatorial Pattern Matching. Lecture Notes in Computer Science. 1264. 1997. str. 116—129. ISBN 978-3-540-63220-7. S2CID 29560680. doi:10.1007/3-540-63220-4. 
  46. ^ Lee, C. Y. (1959). „Representation of Switching Circuits by Binary-Decision Programs”. Bell System Technical Journal. 38 (4): 985—999. doi:10.1002/j.1538-7305.1959.tb01585.x. 
  47. ^ Akers (1978). „Binary Decision Diagrams”. IEEE Transactions on Computers (6): 509—516. S2CID 21028055. doi:10.1109/TC.1978.1675141. 

Literatura uredi

Spoljašnje veze uredi

 
Direktan aciklični graf na Vikimedijinoj ostavi.
Preuzeto iz „https://sr.wikipedia.org/w/index.php?title=Директан_ациклични_граф&oldid=27673103”