Prost delilac

U teoriji brojeva, prosti činioci pozitivnih celih brojeva su prosti brojevi koji dele taj broj tačno .^[1] Prost delilac pozitivnih celih brojeva je lista prostih činioca celog broj, zajedno sa svojim množiocem ; proces određivanja ovih faktora se zove rastavljanje na faktore . Osnovna aritmetička teorema kaže da svaki pozitivan ceo broj ima jednu jedinstvenu osnovnu faktorizaciju.^[2]

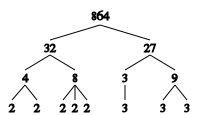
Ova slika pokazuje kako pronaći početno razlaganje broja 864. Stenografski način pisanja nastalih prostih činilaca je 2⁵ × 3³

Skraćivanje prostih faktora, faktori su često izraženi u silama ( umnoženost ) . Na primer,

360=2\times 2\times 2\times 3\times 3\times 5=2^{3}\times 3^{2}\times 5,

u kojem se faktori 2, 3 i 5 umnožavaju od 3, 2 i 1, respektivno.

Za primarni faktor p od n, mnogostrukost p je najveći eksponent a za koje važi p^a deli tačno n puta.

Za pozitivni celi brojevi n, broj glavnih faktora n je zbir glavnih faktora n (ne računajući množilac) su primeri aritmetičkih funkcija n koje su aditivi, ali ne u potpunosti.^[3]

Perfektan kvadrat uredi

Perfektni kvadratni brojevi mogu se prepoznati po tome što svi njihovi osnovni delioce imaju još množilaca. Na primer, broj 144 (kvadrat 12) ima proste činioce

144=2\times 2\times 2\times 2\times 3\times 3=2^{4}\times 3^{2}.

Mogu se preurediti da bi obrazac bio uočljiviji:

144=2\times 2\times 2\times 2\times 3\times 3=(2\times 2\times 3)\times (2\times 2\times 3)=(2\times 2\times 3)^{2}=(12)^{2}.

Zato što svaki osnovni faktor prikazuje paran broj puta, originalni broj se može izraziti kao kvadrat nekog manjeg broja. Na isti način, potpun kub brojeva će imati proste činioce koji su višestruki deljivi sa tri, i tako dalje.

Uzajamno prosti celi brojevi uredi

Za pozitivni cele brojevi bez prostih faktora u zajednički se kaže da su uzajamno prosti. Dva cela broja a i b se takođe mogu definisati kao uzajamno prosti ako je njihov najveći zajednički delilac nzd (a, b) = 1. Euklidov algoritam može da se koristi za određivanje da li su dva cela broja uzajamno prosta, ne znajući njihove proste činioce; algoritam radi u vremenu koje je polinom broja cifara koji su uključeni.

Ceo broj 1 je uzajamno prost svakom pozitivnom celom broju, uključujući i sebe. To je zato što nema proste činioce; to je prazan proizvod. To znači da je nzd (1, b) = 1 za bilo koji b ≥ 1.

Kriptografske aplikacije uredi

Određivanje prostih činioca jednog broja je čest primer problema koji se koristi kako bi se osigurali kriptografski sistemi;^[4] veruje se da ovaj problem zahteva super polinomsko vreme u broju cifara - relativno je lako izgraditi problem koji bi trajao duže nego poznata starost univerzuma da reši problem o aktuelnim računarima koji koriste postojeće algoritme.

Omega funkcije uredi

Funkcija, ω (n) (omega), predstavlja broj različitih prostih činilaca n, Ω (n) (velika omega), predstavlja ukupan broj prostih činilaca n $n$ .^[2] Ako

n=\prod _{i=1}^{\omega (n)}p_{i}^{\alpha _{i}}

,

tada

\Omega (n)=\sum _{i=1}^{\omega (n)}\alpha _{i}

.

Na primer, $24 = 2 3 \times 3 1$ , pa je $ω(24) = 2$ i $Ω(24) = 3 + 1 = 4$ .

$ω(n)$ za $n$ = 1, 2, 3, … je redom 0, 1, 1, 1, 1, 2, 1, 1, 1, … (sekvenca A001221 u OEIS)
$Ω(n)$ for $n$ = 1, 2, 3, … je redom 0, 1, 1, 2, 1, 2, 1, 3, 2, … (sekvenca A001221 u OEIS)

Najmanji prirodan broj k>2^n takav da je sum(ω(k+l), l in [0..n-1])=sum(ω(m), m in [1..n])+n za n=0,1, ... je 2, 3, 5, 10, 18, 33, 66, 134, 262, 521, 1046, 2095, 4797, 8741, 20476, 43311, ..., gde je sledeći termin veći od milion i manji od 8.8*10^19. Po GRH, gornja granica se može poboljšati na 16^17. Ova sekvenca je beskonačna.

n=12, k=116984583*;

n=13, k=135139957 i

n=14, k=810301192936

jesu rešenja jednakosti gore.

Zvezdicom su označeni brojevi k takvi da nijedan od k i k+n-1 nije prosta snaga.

Vidi još uredi

Reference uredi

^ Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.
^ ^a ^b Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9
^ Melvyn B. Nathanson (1996). Additive Number Theory: the Classical Bases. Graduate Texts in Mathematics. 164. Springer-Verlag. ISBN 978-0-387-94656-6.
^ Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. (1996). Handbook of Applied Cryptography. CRC Press. ISBN 978-0-8493-8523-0.

Literatura uredi

Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.

[1] Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.

[Riesel-2] Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9

[3] Melvyn B. Nathanson (1996). Additive Number Theory: the Classical Bases. Graduate Texts in Mathematics. 164. Springer-Verlag. ISBN 978-0-387-94656-6.

[4] Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. (1996). Handbook of Applied Cryptography. CRC Press. ISBN 978-0-8493-8523-0.

[1]

[2]

[3]

[4]