Прост делилац

У теорији бројева, прости чиниоци позитивних целих бројева су прости бројеви који деле тај број тачно .^[1] Прост делилац позитивних целих бројева је листа простих чиниоца целог број, заједно са својим множиоцем ; процес одређивања ових фактора се зове растављање на факторе . Основна аритметичка теорема каже да сваки позитиван цео број има једну јединствену основну факторизацију.^[2]

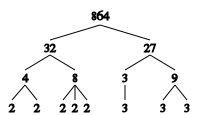
Ова слика показује како пронаћи почетно разлагање броја 864. Стенографски начин писања насталих простих чинилаца је 2⁵ × 3³

Скраћивање простих фактора, фактори су често изражени у силама ( умноженост ) . На пример,

360=2\times 2\times 2\times 3\times 3\times 5=2^{3}\times 3^{2}\times 5,

у којем се фактори 2, 3 и 5 умножавају од 3, 2 и 1, респективно.

За примарни фактор п од н, многострукост п је највећи експонент а за које важи п^a дели тачно н пута.

За позитивни цели бројеви н, број главних фактора н је збир главних фактора н (не рачунајући множилац) су примери аритметичких функција н које су адитиви, али не у потпуности.^[3]

Перфектан квадрат уреди

Перфектни квадратни бројеви могу се препознати по томе што сви њихови основни делиоце имају још множилаца. На пример, број 144 (квадрат 12) има просте чиниоце

144=2\times 2\times 2\times 2\times 3\times 3=2^{4}\times 3^{2}.

Могу се преуредити да би образац био уочљивији:

144=2\times 2\times 2\times 2\times 3\times 3=(2\times 2\times 3)\times (2\times 2\times 3)=(2\times 2\times 3)^{2}=(12)^{2}.

Зато што сваки основни фактор приказује паран број пута, оригинални број се може изразити као квадрат неког мањег броја. На исти начин, потпун куб бројева ће имати просте чиниоце који су вишеструки дељиви са три, и тако даље.

Узајамно прости цели бројеви уреди

За позитивни целе бројеви без простих фактора у заједнички се каже да су узајамно прости. Два цела броја а и б се такође могу дефинисати као узајамно прости ако је њихов највећи заједнички делилац нзд (а, б) = 1. Еуклидов алгоритам може да се користи за одређивање да ли су два цела броја узајамно проста, не знајући њихове просте чиниоце; алгоритам ради у времену које је полином броја цифара који су укључени.

Цео број 1 је узајамно прост сваком позитивном целом броју, укључујући и себе. То је зато што нема просте чиниоце; то је празан производ. То значи да је нзд (1, б) = 1 за било који б ≥ 1.

Криптографске апликације уреди

Одређивање простих чиниоца једног броја је чест пример проблема који се користи како би се осигурали криптографски системи;^[4] верује се да овај проблем захтева супер полиномско време у броју цифара - релативно је лако изградити проблем који би трајао дуже него позната старост универзума да реши проблем о актуелним рачунарима који користе постојеће алгоритме.

Омега функције уреди

Функција, ω (н) (омега), представља број различитих простих чинилаца н, Ω (н) (велика омега), представља укупан број простих чинилаца н $n$ .^[2] Ако

n=\prod _{i=1}^{\omega (n)}p_{i}^{\alpha _{i}}

,

тада

\Omega (n)=\sum _{i=1}^{\omega (n)}\alpha _{i}

.

На пример, $24 = 2 3 \times 3 1$ , па је $ω(24) = 2$ и $Ω(24) = 3 + 1 = 4$ .

$ω(n)$ за $n$ = 1, 2, 3, … је редом 0, 1, 1, 1, 1, 2, 1, 1, 1, … (секвенца А001221 у ОЕИС)
$Ω(n)$ for $n$ = 1, 2, 3, … је редом 0, 1, 1, 2, 1, 2, 1, 3, 2, … (секвенца А001221 у ОЕИС)

Најмањи природан број k>2^n такав да је sum(ω(k+l), l in [0..n-1])=sum(ω(m), m in [1..n])+n за n=0,1, ... је 2, 3, 5, 10, 18, 33, 66, 134, 262, 521, 1046, 2095, 4797, 8741, 20476, 43311, ..., где је следећи термин већи од милион и мањи од 8.8*10^19. По GRH, горња граница се може побољшати на 16^17. Ова секвенца је бесконачна.

n=12, k=116984583*;

n=13, k=135139957 и

n=14, k=810301192936

јесу решења једнакости горе.

Звездицом су означени бројеви k такви да ниједан од k и k+n-1 није проста снага.

Види још уреди

Референце уреди

^ Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.
^ ^а ^б Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9
^ Melvyn B. Nathanson (1996). Additive Number Theory: the Classical Bases. Graduate Texts in Mathematics. 164. Springer-Verlag. ISBN 978-0-387-94656-6.
^ Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. (1996). Handbook of Applied Cryptography. CRC Press. ISBN 978-0-8493-8523-0.

Литература уреди

Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.

[1] Jensen, Gary R. (2004). Arithmetic for Teachers: With Applications and Topics from Geometry. American Mathematical Society.

[Riesel-2] а ^б Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9

[3] Melvyn B. Nathanson (1996). Additive Number Theory: the Classical Bases. Graduate Texts in Mathematics. 164. Springer-Verlag. ISBN 978-0-387-94656-6.

[4] Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. (1996). Handbook of Applied Cryptography. CRC Press. ISBN 978-0-8493-8523-0.

[1]

[2]

[3]

[4]