Електрична струја
Електрична струја је усмерено кретање наелектрисања под утицајем електричног поља или разлике електричних потенцијала. СИ јединица за електричну струју је ампер (А), што је једнако протоку једног кулона наелектрисања у секунди.[2]
| Електрична струја | |
|---|---|
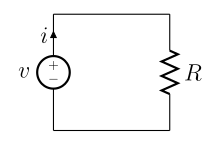 Једноставно електрично коло, у коме је струја приказана ознаком i. Однос између напона (V), отпора (R), и јачине струје (I) је V = IR; то је познато као Омов закон.[1] | |
Уобичајени симболи | I |
| СИ јединица | ампер |
| СИ димензија | |
Деривације из других квантитета | |
Електрична струја може бити једносмерна или наизменична.[3][4] Струја тече кроз метале, електролите, гасове и полупроводнике. Носиоци набоја у металима су слободни електрони, у електролитима негативни и позитивни јони (анјони и катјони), у гасовима јони и електрони, а у полупроводницима електрони и шупљине.[5]
Метали који обилују слободним електронима су добри проводници струје, нпр. сребро, бакар и злато. Слободни електрони су они електрони који нису у атому, нпр. однос слободних и неслободних електрона у бакру је 1:1, а то значи да на сваки кубни центиметар бакра долази 1×1022 слободних електрона, па се бакар одликује добром проводношћу.
Договором је одређен технички смер струје као смер кретања позитивног набоја (од позитивног према негативном полу). Како се електрони крећу у супротном смеру, то значи да је њихов набој негативан.
Електрони се у проводнику усмерено крећу под утицајем електричног поља, па због тога на крајевима проводника мора постојати разлика потенцијала, тј. напон. Кад нема електричног поља, кретање електрона је хаотично, што значи да је сваки смер једнако могућ и то брзином од око 1000 km/s (средња термичка брзина). Деловањем електричног поља електрони добијају додатну заједничку компоненту брзине кретања према позитивном полу (клизање) од свега неколико mm/s (дрифтна брзина).
Количина набоја Q у неком проводнику једнака је умношку набоја електрона e и броја тих електрона N:
Симбол уреди
Конвенционални симбол за струју је I, што потиче од француске фразе intensité de courant, (јачина струје).[6][7] Јачина струје се обично назива једноставно струјом.[8] Симбол I је користио Андре-Мари Ампер, по коме је названа јединица електричне струје, у формулацији закона Амперове силе (1820).[9][10][11] Та нотација је прихваћена у Великој Британији, где је постала стандард, мада постоји бар један часопис у коме је кориштено C уместо I до 1896.[12]
Дефиниција уреди
Интензитет електричне струје се дефинише као количник протекле количине наелектрисања у јединици времена, односно математички формализовано као извод по времену наелектрисања:[13]
Строже, струја се посматра као величина зависна од времена, јер током времена може протицати променљива количина наелектрисања:
- или инверзно као
што се тумачи да је количина наелектрисања затечена у једном тренутку једнака збиру свих дотока струје до тог тренутка.
Количина наелектрисања Q која протекне у јединици времена t је I, што потиче од француске речи за струју intensité.
Струја у класичним чврстим проводницима уреди
У већини чврстих проводника, када на њих не делују спољне електричне силе, постоји насумично кретање слободних електрона које настаје услед термалне енергије коју електрони добијају из околног простора. Када атом изгуби слободни електрон, постаје позитивно наелектрисан. Слободан електрон може да се креће међу овим позитивним јонима, док они могу само да осцилују око њихових сталних места у решетки проводника. Слободни електрони су стога носиоци наелектрисања у чврстим проводницима. Ако се замисли раван која пресеца проводник на пола, укупан број слободних наелектрисања (електрона) који пролазе са једне стране на другу једнак је броју који пролази у супротном смеру.
Када се крајеви чврстог проводника споје са половима извора напона, на пример једносмерне струје као што је батерија, тај извор успоставља електрично поље кроз проводник. У тренутку спајања контаката, слободни електрони у проводнику ће почети да се крећу ка позитивном крају извора под утицајем електричног поља. За сваки ампер струје, 1 кулон наелектрисања (који се састоји од око 6.242 × елементарних наелектрисања - наелектрисање једног електрона или протона) пролази сваке секунде кроз попречни пресек проводника.
Струја у амперима се може израчунати из следеће једначине:
где је
Следи да је:
- и
Електрична отпорност проводника уреди
Електрична отпорност отпорника зависи од специфичне отпорности проводника, сразмерна је његовој дужини и обрнуто сразмерна његовој површини попречног пресека R је сразмерно l
Где је R је електрична отпорност, Ro је специфична отпорност проводника, l је дужина проводника, S је површина попречног пресека.
Просечна брзина наелектрисања уреди
Покретна наелектрисања унутар проводника стално се крећу у насумичним правцима. Електрони су носиоци наелектрисања у металима. Непрестано се сударају са непокретним атомима и мењају свој смер и правац кретања. Ако се у обзир узме брзина кретања електрона у облику вектора, просечна брзина свих електрона заједно у проводнику је једнака нули. Ово је зато што се крећу у свим правцима и смеровима, који се међусобно поништавају. Иако се у сваком проводнику електрони непрестано крећу, не може се увек говорити о постојању електричне струје. Када се проводник нађе у електричном пољу, електрони у њему почињу да се крећу усмерено под утицајем поља. И даље се крећу неправилно, сударају се са атомима и мењају свој смер и правац кретања, али просечна брзина је сада различита од нуле, и крећу се у правцу електричног поља. Ова просечна брзина се у литератури још назива и „брзина дрифта“. Брзина којом се крећу може се израчунати из израза:
где је:
- електрична струја
- број носилаца наелектрисања по јединици запремине
- површина попречног пресека проводника
- просечна брзина наелектрисања
- количина наелектрисања једног носиоца.
Брзина електричне струје у чврстом проводнику је обично веома мала. На пример, у бакарној жици, попречног пресека 0.5 mm², са струјом од 5 A, просечна брзина електрона је реда милиметра у секунди. Насупрот томе, на пример, у катодној цеви, електрони се крећу у приближно правој линији брзином од десетог дела брзине светлости.
Иначе, зна се да је сигнал електричне струје талас, који пропагира дуж проводника великом брзином. Као што је то са таласима, брзина таласа у некој материји има мало везе са брзином те материје, док се креће кроз њу. На пример, у преносним мрежама наизменичне струје, талас струје се креће веома брзо од извора до удаљеног потрошача, док се наелектрисања у проводнику само померају напред-назад у малим растојањима. Брзина наелектрисања може бити веома мала, а опет, било које наелектрисање у струји се може кретати брзином светлости, мада у неким материјалима може бити и спорије.
Омов закон уреди
Омов закон, један од основних закона у области електричне струје, предвиђа да електрична струја у идеалном отпорнику или неком другом резистивном (отпорном) елементу буде једнака количнику електричног напона на елементу и електричног отпора:[14][15][16][17]
где је:
- I електрична струја, мерена у амперима (А)
- U електрични напон, мерен у волтима (V)
- R је електрични отпор у омима. (Ω)
Специфичније, из Омовог закона дефинисаног овом релацијом следи да је отпор константан и независан од струје.[1]
Густина струје и Омов закон уреди
Густина струје је мера густине електричне струје. Она се дефинише као вектор чија магнитуда је електрична струја по попречном пресеку. У СИ јединицама, густина струје се изражава у амперима по квадратном метру.
где је струја у проводнику, је густина струје, и је диференцијални вектор области попречног пресека.
Густина струје (струја по јединици површине) код материјала са коначним отпором је директно пропорционална електричном пољу медијума. Константа пропорционалности се назива проводљивост материјала, и њена вредност је зависна од природе датог материјала, и најчешће од температуре материјала:
Реципрочна вредност проводљивости материјала је отпорност материјала и горња једначина написана у погледу отпора постаје:
- или
Проводност код полупроводничких уређаја се може јавити као комбинација дрифта и дифузије, која је пропорционална са константом дифузије и густином електричног набоја . Густина струје је онда:
где је елементарно наелектрисање а густина електрона. Преносиоци се крећу у смеру опадајуће концентрације, тако да за електроне позитивна струја производи позитивни градијент густине. Ако су преносници шупљине, густина електрона се замењује негативном густином шупљина .
Код линеарних анизотропних материјала, σ, ρ и D су тензори.[18]
Код линеарних материјала као што су метали, при ниским фреквенцијама, густина струје кроз површину проводника је униформна. У таквим условима, Омов закон наводи да је струја директно пропорционална разлици потенцијала између два краја тог металног (идеалног) проводника (или другог омског уређаја): . Код наизменичних струја, посебно при високим фреквенцијама, скин ефекат узрокује неравномерно простирање струје дуж попречног пресека проводника, при чем се већа густина јавља уз површину, чиме се повећава појавна отпорност.[19][20]
Конвенционални смер струје уреди
Конвенционални смер струје је дефинисан још на почетку развоја електротехнике као једнак току позитивног наелектрисања. Односно, усвојено је да струја увек тече од позитивног пола извора напона, ка негативном полу. У чврстим металима, као што су жице, позитивна наелектрисања су непокретна, а само негативна наелектрисања теку у смеру супротном конвенционалној струји, мада то није случај у неким не-металним проводницима. Електрична струја у електролитима је ток наелектрисаних атома (јона), који могу бити и позитивно и негативно наелектрисани. Такав је случај проласка струје кроз водени раствор кухињске соли или воде за пиће која природно садржи у себи растворе различитих минерала, док чиста или дестилована вода не проводи струју јер не садржи у себи јоне. Такође, занимљив је и пример, електрохемијске ћелије која може бити направљена уз помоћ слане воде (раствор натријум хлорида) са једне стране мембране и свеже воде са друге. Мембрана дозвољава пролаз позитивним јонима натријума, али не и негативним јонима хлорида, тако да постоји електрична струја кроз мембрану. Електрична струја у плазми је ток електрона као и позитивних и негативних јона. У леду, и неким чврстим електролитима, ток протона ствара електричну струју. Очигледно је да у различитим материјалима, струју чине различити носиоци наелектрисања, па чак и у неким материјалима постоји неколико различитих носилаца наелектрисања, који могу тећи у различитим смеровима. Да би се поједноставила ова ситуација задржана је оригинална дефиниција конвенционалног смера струје.
Постоје и примери где су електрони ти који се покрећу, али има више смисла да се та струја посматра као ток позитивних „електронских шупљина“ (недостатак једног електрона у омотачу да би атом био неутрално наелектрисан). Ово је случај код полупроводника П-типа.[21]
Референтан смер уреди
Приликом анализе електричних кола, могуће је да прави смер струје у неком елементу кола није познат. Стога, за струје са непознатим смером, усваја се, произвољно, референтан смер. Након што се нађу стварне вредности струја у колу, поједине струје могу имати и негативне интензитете. Дакле, за негативно добијене струје, њихов прави смер је супротан од референтног који је усвојен пре решавања кола.[22]
Електромагнетизам уреди
Свака електрична струја ствара магнетско поље. Магнетско поље се може представити затвореним кружним линијама који окружују проводника.[27][28]
Електрична струја се непосредно може мерити галванометром,[29] али та метода захтева претходно прекидање кола, што је непрактично у неким случајевима. Електрична струја се понекада може измерити и без прекидања кола, детектовањем и мерењем магнетског поља око проводника. Неки од таквих уређаја су сензори Халовог ефекта,[30] струјни трансформатори и калеми Роговског.[31][32]
Електромагнет уреди
Електромагнетни калем, са великим бројем кружних намотаја изоловане жице омотаних око цилиндричне основе, понаша се као магнет кад електрична струја протиче кроз њега. Кад се струја искључи, калем моментално губи свој магнетизам. Такав уређај се назива електромагнетом.[33] Електрична струја производи магнетно поље. Оно се може приказати у виду кружних линија поља које окружују жице, и које постоји докле год има протока струје.
Магнетизам исто тако може да произведе електричну струју. Кад се променљиво магнетно поље примени на проводник, настаје електромоторна сила (ЕМФ) и кад постоји подесан пут то узрокује настанак струје.[34][35]
Радио таласи уреди
Кад електрична струја протиче кроз подесно обликовани проводник на радио фреквенцијама може да дође до формирања радио таласа.[36] Они путују брзином светлости и могу да узрокују појаву електричне струје у удаљеним проводницима.[37]
Види још уреди
Референце уреди
- ^ а б Heaviside, Oliver (1894). Electrical papers. 1. Macmillan and Co. стр. 283. ISBN 978-0-8218-2840-3.
- ^ Lakatos, John; Oenoki, Keiji; Judez, Hector; Oenoki, Kazushi; Hyun Kyu Cho (1998). „Learn Physics Today!”. Lima, Peru: Colegio Dr. Franklin D. Roosevelt. Архивирано из оригинала 27. 2. 2009. г. Приступљено 10. 3. 2009.
- ^ Bhargava & Kulshreshtha 1983, стр. 90 harvnb грешка: више циљева (2×): CITEREFBhargavaKulshreshtha1983 (help)
- ^ National Electric Light Association (1915). Electrical meterman's handbook. Trow Press. стр. 81.
- ^ Fischer, Anthony C.-Cripps (2004). The electronics companion. CRC Press. стр. 13. ISBN 978-0-7503-1012-3.
- ^ Lowe & Rounce 2002, стр. 2
- ^ Berlin, Howard M.; Frank C. Getz (1988). Principles of Electronic Instrumentation and Measurement. Merrill Pub. Co. стр. 37. ISBN 978-0-675-20449-1.
- ^ K. S. Suresh Kumar (2013). 'Electric Circuit Analysis. Pearson Education India. ISBN 978-9332514102.
- ^ A-M Ampère, Recueil d'Observations Électro-dynamiques. pp. 56, Paris: Chez Crochard Libraire 1822 (in French).
- ^ Serway & Jewett 2006, стр. 746
- ^ Monk 2004, стр. 16
- ^ Electric Power, vol. 6. ] Electric Power. 1894. стр. 411.
- ^ Popović, Branko (1989). „Vremenski konstante električne struje”. Osnovi elektrotehnike I (8 изд.). Beograd: Građevinska knjiga. стр. 182—183. ISBN 86-395-0176 Проверите вредност параметра
|isbn=: length (помоћ). - ^ Consoliver, Earl L.; Mitchell, Grover I. (1920). Automotive ignition systems. McGraw-Hill. стр. 4.
- ^ Purcell 1985, стр. 129
- ^ а б Griffiths, David J. (1999). Introduction to electrodynamics (3rd изд.). Prentice Hall. стр. 289. ISBN 978-0-13-805326-0.
- ^ Millikan 1917, стр. 54
- ^ „What is a Tensor?”. Dissemination of IT for the Promotion of Materials Science. University of Cambridge.
- ^ Fink & Beaty 2000, стр. 2–50
- ^ Hayt, William H. (1989). Engineering Electromagnetics (5th изд.). McGraw-Hill. стр. 362. ISBN 978-0-07-027406-8.
- ^ Ashcroft & Mermin 1976, стр. 299–302
- ^ Robinson & Snyder-Mackler 2007, стр. 10.
- ^ John David Jackson (1999). Classical Electrodynamics (3rd изд.). Wiley. стр. 238. ISBN 978-0-471-30932-1.
- ^ Owen, George E. (2003). op. cit.. Mineola, N.Y.: Dover Publications. стр. 285. ISBN 978-0-486-42830-7.
- ^ J. Billingham; A. C. King (2006). Wave Motion. Cambridge University Press. стр. 179. ISBN 978-0-521-63450-2.
- ^ J.C. Slater and N.H. Frank (1969). Electromagnetism (Reprint of 1947 изд.). Courier Dover Publications. стр. 83. ISBN 978-0-486-62263-7.
- ^ Jiles 1998, стр. 2
- ^ Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew (1964). The Feynman Lectures on Physics. 2. California Institute of Technology. ISBN 978-0-465-07998-8. Архивирано из оригинала 02. 12. 2016. г. Приступљено 07. 06. 2017.
- ^ „Theory of Galvanometer”. Приступљено 5. 4. 2017.
- ^ „An Overview Of Clamp Meter”. 6. 5. 2012.
- ^ John G. Webster, Halit Eren, ур. (2014). Measurement, Instrumentation, and Sensors Handbook, Second Edition: Electromagnetic, Optical, Radiation, Chemical, and Biomedical Measurement. CRC Press. стр. 16—6. ISBN 978-1-4398-4891-3. to 16-7.
- ^ Schon, Klaus (2013). High Impulse Voltage and Current Measurement Techniques: Fundamentals – Measuring Instruments – Measuring Methods. Springer Science & Business Media. стр. 193. ISBN 978-3-319-00378-8.
- ^ Banerjee 2015.
- ^ Langmuir, Irving (1916). „The Relation Between Contact Potentials and Electrochemical Action”. Transactions of the American Electrochemical Society. The Society. 29: 125—182.
- ^ Tipler 1976, стр. 803.
- ^ Graf 1999, стр. 29
- ^ Stutzman, Warren L.; Thiele, Gary A. (2012). Antenna Theory and Design, 3rd Ed. John Wiley & Sons. ISBN 978-0-470-57664-9.
Литература уреди
- Schon, Klaus (2013). High Impulse Voltage and Current Measurement Techniques: Fundamentals – Measuring Instruments – Measuring Methods. Springer Science & Business Media. стр. 193. ISBN 978-3-319-00378-8.
- K. S. Suresh Kumar (2013). 'Electric Circuit Analysis. Pearson Education India. ISBN 978-9332514102.
- Berlin, Howard M.; Frank C. Getz (1988). Principles of Electronic Instrumentation and Measurement. Merrill Pub. Co. стр. 37. ISBN 978-0-675-20449-1.
- Lowe, T. L.; Rounce, John (2002). Calculations for A-level Physics. Nelson Thornes. стр. 2. ISBN 978-0-7487-6748-9.
- Consoliver, Earl L.; Mitchell, Grover I. (1920). Automotive ignition systems. McGraw-Hill. стр. 4.
- John G. Webster, Halit Eren, ур. (2014). Measurement, Instrumentation, and Sensors Handbook, Second Edition: Electromagnetic, Optical, Radiation, Chemical, and Biomedical Measurement. CRC Press. стр. 16—6 to 16—7. ISBN 978-1-4398-4891-3.
- Griffiths, David J. (1999). Introduction to electrodynamics (3rd изд.). Prentice Hall. стр. 289. ISBN 978-0-13-805326-0.
- Purcell, Edward M. (1985). Electricity and magnetism. Berkeley Physics Course. 2 (2nd изд.). McGraw-Hill. стр. 129. ISBN 978-0-07-004908-6.
- Millikan, Robert A. (1917). Elements of Electricity. American Technical Society. стр. 54.
- Heaviside, Oliver (1894). Electrical papers. 1. Macmillan and Co. стр. 283. ISBN 978-0-8218-2840-3.
- Banerjee, Chandana (2015). We And Our World (First изд.). Bharati Bhawan. ISBN 978-81-7709-720-7.
- Graf, Rudolf F. (1999). Modern Dictionary of Electronics. Newnes. стр. 29. ISBN 978-0-7506-9866-5.
- Stutzman, Warren L.; Thiele, Gary A. (2012). Antenna Theory and Design, 3rd Ed. John Wiley & Sons. стр. 560—564. ISBN 978-0-470-57664-9.
- Tipler, Paul A. (1976). Physics. New York, NY: Worth Publishers, Inc. стр. 803. ISBN 978-0-87901-041-6.
- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew (1964). The Feynman Lectures on Physics. 2. California Institute of Technology. ISBN 978-0-465-07998-8. Архивирано из оригинала 02. 12. 2016. г. Приступљено 07. 06. 2017.
- Jiles, David C. (1998). Introduction to Magnetism and Magnetic Materials (2 изд.). CRC. стр. 3. ISBN 978-0-412-79860-3.
- Robinson, Andrew J.; Snyder-Mackler, Lynn (2007). Clinical Electrophysiology: Electrotherapy and Electrophysiologic Testing (3rd изд.). Lippincott Williams & Wilkins. стр. 10. ISBN 978-0-7817-4484-3.
- Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics (1st изд.). Holt, Reinhart, and Winston. стр. 299-302. ISBN 978-0-03-083993-1. Приступљено 17. 1. 2017.
- Fink, Donald G.; Beaty, H. Wayne (2000). Standard Handbook for Electrical Engineers (14th изд.). McGraw-Hill. стр. 2–50. ISBN 978-0-07-022005-8.
- Hayt, William H. (1989). Engineering Electromagnetics (5th изд.). McGraw-Hill. ISBN 978-0-07-027406-8.
- Monk, Paul S. M. (2004). Physical chemistry: understanding our chemical world. New York: Chichester: Wiley. стр. 16. ISBN 978-0-471-49181-1.
- Serway, Raymond A.; Jewett, J. W. (2006). Serway's principles of physics: a calculus based text (Fourth изд.). Belmont, California: Thompson Brooks/Cole. стр. 746. ISBN 978-0-534-49143-7.
- Bhargava, N. N.; Kulshreshtha, D. C. (1983). Basic Electronics & Linear Circuits. Tata McGraw-Hill Education. стр. 90. ISBN 978-0-07-451965-3. Непознати параметар
|name-list-style=игнорисан (помоћ) - National Electric Light Association (1915). Electrical meterman's handbook. Trow Press. стр. 81.
- Bhargava, N. N.; Kulshreshtha, D. C. (1983). Basic Electronics & Linear Circuits. Tata McGraw-Hill Education. стр. 90. ISBN 978-0-07-451965-3. Непознати параметар
|name-list-style=игнорисан (помоћ) - Millikan, Robert A.; Bishop, E. S. (1917). Elements of Electricity. American Technical Society. стр. 54.
- Consoliver, Earl L.; Mitchell, Grover I. (1920). Automotive ignition systems. McGraw-Hill. стр. 4.
- Shedd, John C.; Hershey, Mayo D. (1913). „Popular Science”. Bonnier Corporation. стр. 599. ISBN 01617370.
- Schagrin, Morton L. (1963). „Resistance to Ohm's Law”. American Journal of Physics. 31 (7): 536—47. Bibcode:1963AmJPh..31..536S. doi:10.1119/1.1969620.
- Muller, Richard S.; Kamins, Theodore I. (1986). Device Electronics for Integrated Circuits. John Wiley and Sons. ISBN 978-0-471-88758-4. Непознати параметар
|name-list-style=игнорисан (помоћ)
Спољашње везе уреди
- Интерактивна конверзија јединица Архивирано на сајту Wayback Machine (5. децембар 2008) - конверзија једне јединице у друге јединице струје
- У ком смеру наелектрисање заиста тече?
- Све о електричним колима - користан сајт за упознавање са електрицитетом и електроником.


