Орбита
Као појам у физици, орбита је пут које једно тело чини око другог тела док је под утицајем неке силе.[1] Орбите је први изучавао Јохан Кеплер који је открио Кеплерове законе о кретању планета (в. Други Кеплеров закон). Орбите могу бити кружне, параболичне, елиптичне, хиперболичне, а планете круже око Сунца по елипси (види ексцентрицитет). Свака орбита је одређена са орбиталним елементима који тачно описују орбиту, као и положај тела на њој. Орбиталних елемената има шест и они су: ексцентрицитет, велика полуоса, инклинација, лонгитуда узлазног чвора, аргумент перихела и права аномалија.






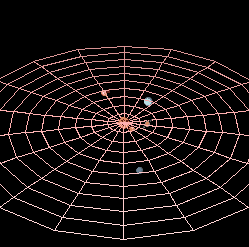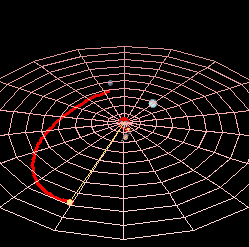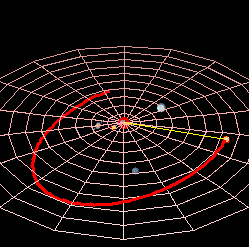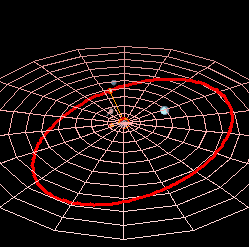


Планетарна путања у астрономији и астронаутици, је путања у облику конике по којој се креће небеско тело мање масе у гравитационом пољу небеског тела веће масе. Затворена орбита небеских тела елипса је са жариштем у којем се налази средишње физичко тело или средиште масе. Такве су орбите планета и њихових природних сателита у Сунчевом систему. Затворена орбита небеских тела елипса је са жариштем у којем се налази средишње физичко тело или средиште масе. Такве су орбите планета и њихових природних сателита у Сунчевом систему. Отворена орбита је парабола (на пример орбита неких комета) или хипербола.
Орбите вештачких сателита, које могу бити кружне или елиптичне, означавају се с обзиром на начин кретања око Земље:
- геосинхрона орбита има период 1 дан, док је геостационарна орбита она геосинхрона орбита којом се сателит поставља изнад истог положаја на Земљиној површини;
- поларна орбита, односно квазиполарна орбита, прелази преко полова, односно близу њих;
- са Сунцем синхронизована орбита има раван увек уперену у Сунце или под сталним угаоним одмаком од Сунца, а сателит прелази преко екватора увек у исто доба дана;
- прелазна орбита, уведена ради економичности, орбита је између почетне и коначне орбите при постављању вештачких сателита.
- орбита за паркирање привремена је орбита вештачког сателита;
- пролећна орбита је орбита којом свемирска летелица пролази покрај небеског тела (на пример Месеца или неке планете).[2]
Јохан Кеплер је први пронашао своје законе планетарног кретања. Открио је да су путање планета у нашем Сунчевом систему елиптичне.
Први Кеплеров закон и планетарне путање
уредиПрви Кеплеров закон утврђује геометријске особине планетарних путања. Ј. Кеплер је нашао да су стазе елипсе, а да се Сунце налази у једном од жаришта.[3] Како је Сунце заједничко свим планетима, тако је Сунце у жаришту које је заједничко свим елиптичним стазама. То је једини услов и нема даљих ограничења, те положај путање у простору може бити веома разнолик. На скицама које приказују две или више планетарних путања, оне се налазе у истој равни. Генерално, велике полуосе две елипсе се не подударају ни по смеру, ни по величини, ни по равнима у којима се налазе.
Величина и издуженост елипсе одређена је великом полуосом a и ексцентрицитетом e. Велика полуоса a уједно је и средња удаљеност тачке на елипси од једног жаришта (планета од Сунца). Када је тело најдаље од Сунца у афелу, његова је проводница (радијусвектор) највећа и износи:
Када је планета најближа Сунцу (када је у перихелу), тада јој је проводница најмања и износи:
Аритметичка средина највеће и најмање удаљености планете од Сунца или средња удаљеност једнака је великој полуоси a:
Издуженост путање исказује се нумеричким ексцентрицитетом ε који је једнак односу линеарног ексцентрицитета и велике полуосе стазе:
ε је бездимензионална величина. Са смањењењем ексцентрицитета (ε → 0) елипса прелази у кружницу, а њена велика полуоса прелази у полупречник кружнице. Улогу средње удаљености има тада, наравно, сам полупречник кружнице. С друге стране, с повећањем ексцентрицитета (ε → 1) елипса прелази у параболу. За хиперболу вреди ε > 1. Парабола и хипербола нису затворене криве.
Величине планетарних путања
уредиПоложај планетарне путање у простору треба одредити помоћу познатих оријентира. Зато се употребљава раван еклиптике и пролећна тачка. Угао између равни у којој се налази стаза тела и равни еклиптике зове се нагиб или инклинација (ознака: i). Две се равни секу у правцу на којему су две тачке истакнуте - оне у којима планетарна путања пробада раван еклиптике: узлазни чвор Ω (у њему тело у свом годишњем кретању прелази са јужне стране еклиптике на северну) и силазни чвор Ʊ (у њему тело у свом годишњем кретању прелази са северне стране еклиптике на јужну). Положај узлазног чвора задаје се еклиптичком дужином узлазног чвора Ω. С мерама i и Ω оријентисана је раван кретања небеског тела у простору. Да би се у тој равни оријентисала елипса, бељежи се положај њеног перихела. У ту сврху служи аргумент перихела π, угао од узлазног чвора до велике полуосе која садржи перихел. Лонгитудом перихела назива се укупан угао ω = Ω + π.
Да би се пратило кретање небеског тела, потребно је додати податак о звезданом (сидеричком) опходном времену P и о тренутку to у којем тело пролази перихелом. Дакле, за опис геометријских својстава планетарних путања - величине елипсе, облика елипсе, њене оријентације и начина кретења тела - потребно је 7 величина: a, e, i, Ω, ω, P и to. То су величине планетарних путања.
Анализа планетарних путања
уредиВећина планета има слабо издужене планетарне путање (стазе), које је на малом цртежу оком тешко разликовати од кружнице. Тако Земљина путања с ε = 0,001673 има велику полуосу a = 149,597 ∙ 106 km, малу полуосу b = 149,577 ∙ 106 km, најмању удаљеност од Сунца rmin = 147,1 ∙ 106 km и највећу удаљеност од Сунца rmax = 152.1 ∙ 106 km.
Стазе планетоида у просеку су јаче издужене ос планетних путања. Код комета је шароликост много већа. Неке комете имају нумерички ексцентрицитет ε близак јединици.
Најиздуженију стазу има Меркур (e = 0,205), док најмањи ексцентрицитет има Венера (e = 0,007).
Разлике се опажају и у нагибима планетарних путања. Плутонова и Меркурова стаза највише се од свих планета отклањају од Земљине путање. Код Плутона то доводи до занимљиве последице. Наиме, цртају ли се стазе Нептуна и Плутона пројектоване у исту равнину, чини се да се због издужености Плутонове стазе те две путање секу, те да се две планете могу и сударити. Нептун је заиста у неким раздобљима даље од Сунца него Плутон (на пример као од 1980. до 1999). Међутим како се равни путања Нептуна и Плутона секу под углом од око 15°, те су стазе увек далеко једна од друге. Стога се они никада не могу сударити.
Путање планетоида нагнуте су према еклиптици за више десетина ступњева, равни комета могу сећи еклиптику под било којим углом. Када је угао инклинације већи од 180°, каже се да је путања небеског тела и његова револуција ретроградна; пројектујући такву стазу на раван еклиптике, видело би се да се тело креће око Сунца у супротном смислу од Земље и осталих планета. Све планете и планетоиди имају директну револуцију. Физички различите врсте тела у Сунчевом систему се групишу по геометријским својствима путања. До разлика у владању небеских тела дошло је у току развоја Сунчевог система.
Генерално, величине планетарних путања појединог члана Сунчевог система непрестано се мењају. Промена тих величина код Земље могла је у прошлости, у дугим геолошким раздобљима, утицати на климатске промене.
Може се запазити још да се велика полуоса (линија која повезује најближи и најудаљенији положај тела од Сунца, перихел и афел), названа још и линија апсида, не подудара с линијом која повезује зимску и летњу тачку. Разлика се у ствари стално повећава, јер се линија апсида закреће у линији путање; закреће се у смеру кретања Земље, те Земљи треба више времена да поново стигне у перихел, него што јој треба да понови свој положај према звездама. Другим речима, звездана (сидеричка) година краћа је од времена проласка Земље перихелом. То раздобље траје 365 д 6 h 13 min 53 s = 365,25964 дан и зове се аномалистичка година (година).[4]
Земљина путања
уредиЗемљина путања у астрономији преставља планетарну путању (орбиту) Земље којом обилази Сунце, на удаљености од једне астрономске јединице (АЈ) или 149 597 870 691 ± 30 метара, што преставља приближно 150 милиона километара.[5][6] Перихел Земље је најближа тачка Земљине путање до Сунчевог средишта, смештена на крају велике осе елипсе којом се Земља креће релативно према Сунцу, а Земља пролази кроз перихел сваке године почетком јануара (у задње време 3. јануара) и износи 147 098 291 km. Афел Земље је најудаљенија тачка путање Земље до Сунчевог средишта, а Земља пролази кроз афел почетком јула (у задње време 4. јула) и износи 152 098 233 km. Орбитална брзина Земље је 30 km/s (108 000 km/h) што значи да пређе удаљеност Земљиног пречника (око 12 700 km) за 7 минута или удаљеност до Месеца (око 384 000 km) za 4 sata.
Референце
уреди- ^ Fitzpatrick, Richard (2. 2. 2006). „Planetary orbits”. Classical Mechanics – an introductory course. The University of Texas at Austin. Архивирано из оригинала 3. 3. 2001. г.
- ^ orbita, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2018.
- ^ Wilson, Curtis (мај 1994). „Kepler's Laws, So-Called” (PDF). HAD News (31): 1—2. Приступљено 27. 12. 2016.
- ^ Vladis Vujnović : "Astronomija", Školska knjiga, 1989.
- ^ „Sun: Facts & Figures”. Solar System Exploration. National Aeronautics and Space Administration. Архивирано из оригинала 3. 7. 2015. г. Приступљено 29. 7. 2015.
- ^ Jean Meeus, Astronomical Algorithms 2nd ed, ISBN 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough.
Литература
уреди- Abell; Morrison; Wolff (1987). Exploration of the Universe (fifth изд.). Saunders College Publishing.
- Linton, Christopher (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press. ISBN 978-1-139-45379-0.
- Frank Swetz; John Fauvel; Bengt Johansson; Victor Katz; Otto Bekken (1995). Learn from the Masters. MAA. ISBN 978-0-88385-703-8.
- Andrea Milani and Giovanni F. Gronchi. Theory of Orbit Determination (Cambridge University Press; 378 pages; 2010). Discusses new algorithms for determining the orbits of both natural and artificial celestial bodies.
- Roger, R. Bate; Mueller, Donald D.; White, Jerry E. (1971). Fundamentals of Astrodynamics . Dover Books on Astronomy and Astrophysics. New York: Dover Publications. стр. 21. ISBN 0486600610. LCCN 73157430.
- El'Yasberg "Theory of flight of artificial earth satellites", Israel program for Scientific Translations (1967)
- Bate, Roger; Mueller, Donald; White, Jerry (1971). Fundamentals of Astrodynamics . Dover Publications, Inc., New York. ISBN 0-486-60061-0.
- Copernicus, Nicolaus (1952), „Book I, Chapter 4, The Movement of the Celestial Bodies Is Regular, Circular, and Everlasting-Or Else Compounded of Circular Movements”, On the Revolutions of the Heavenly Spheres, Great Books of the Western World, 16, Превод: Charles Glenn Wallis, Chicago: William Benton, стр. 497—838
Спољашње везе
уреди- CalcTool: Orbital period of a planet calculator. Has wide choice of units. Requires JavaScript.
- Java simulation on orbital motion. Requires Java.
- NOAA page on Climate Forcing Data includes (calculated) data on Earth orbit variations over the last 50 million years and for the coming 20 million years
- On-line orbit plotter. Requires JavaScript.
- Orbital Mechanics (Rocket and Space Technology)
- Orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbit eccentricity, and also a series for orbital inclination. Orbits for the other planets were also calculated, by F. Varadi; B. Runnegar; M. Ghil (2003). „Successive Refinements in Long-Term Integrations of Planetary Orbits”. The Astrophysical Journal. 592 (1): 620—630. Bibcode:2003ApJ...592..620V. doi:10.1086/375560 ., but only the eccentricity data for Earth and Mercury are available online.
- Understand orbits using direct manipulation Архивирано на сајту Wayback Machine (8. новембар 2017). Requires JavaScript and Macromedia
- Merrifield, Michael. „Orbits (including the first manned orbit)”. Sixty Symbols. Brady Haran for the University of Nottingham.
- Planetary orbit Simulator Astronoo