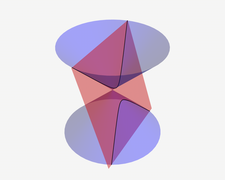
Конусни пресек
Конусни пресеци заузимају веома значајно место како у геометрији, тако и у целој математици. Конусни пресек представља пресек конуса и произвољне равни у простору. Постоје различити случајеви пресека. Деле се на дегенерисане (тачка, права или две праве које се секу), и недегенерисане (криве). Недегенерисани су пресеци код којих раван не садржи теме конуса и такви пресеци се називају конике. Ту спадају парабола, хипербола, елипса, као и специјални случај елипсе - круг. Основна карактеристика недегенерисаних конусних пресека (осим круга) је да постоје тачка (жижа) и права (директриса) такве да је однос растојања произвољне тачке конике до њих константан. У аналитичкој геометрији, коника се може дефинисати као раванска алгебарска крива другог реда. Такође, конике су веома значајне за многе области. На пример, у астрономији: небеска тела се крећу путањама које су заправо конике, у оптици (конструкција сочива и огледала), механици и многим другим областима. Често се примењују и у палеонтологији за разумевање изгледа одређених организама.
-
Елипса
-
Круг
-
Хипербола
-
Парабола
Историја конусних пресека уреди
Стара Грчка уреди
Проучавање конусних пресека датира још од времена старих Грка. Сматра се да је први који је открио, дефинисао и описао конусне пресеке био Менехмо (Menaechmus, око 375—325. године пре нове ере), Платонов ученик и тутор Александра Великог. Мехнемов рад није сачуван тако да данас о њему сазнајемо само из различитих списа његових савременика. Користио је конусне пресеке у покушају решавања три проблема конструктивне геометрије: квадратуре круге, трисекције угла и удвостручавања коцке. Дефиниција која се тада користила се разликује од ове данашње. Тек када је у 19. веку доказано да наведена три проблема нису решива употребом само лењира и шестара, конусни пресеци су почели да се дефинишу као пресеци усправног кружног конуса и равни. У старој Грчкој су конусе конструисали обртањем правоуглог троугла око једне од катета, тако да хипотенуза генерише површину конуса. Конусни пресеци су се добијали конструисањем равни која је пресецала конус. Одређивање конике се вршило тако што се посматрао угао између равни и теменог угла (двоструке величине угла који образују хипотенуза и катета око које се ротира троугао). Уколико је тај угао оштар, коника је елипса, ако је прав, парабола, и уколико је угао туп, у питању је хипербола. Сматра се да се конусним пресецима бавио и Еуклид (Euclid, око 330—275. године пре нове ере), међутим ни његови радови нису сачувани. Конике, са посебним акцентом на параболу, проучавао је и Архимед (Archimedes, 287—212. године пре нове ере). Његови радови попут "Расправе о квадратури параболе" су сачувани до данас.
У проучавању коника посебан допринос је дао Аполоније (Appollonius, око 262—190. године пре нове ере), грчки математичар и астроном. Он је написао монографију "Конусни пресеци" која се састојала од осам књига са 787 ставова. Прве четири књиге су на грчком језику, наредне три на персијском, док је осма, последња, изгубљена. Аполоније је први који је дао основне теорије о све три конике на кружном, усправном или косом конусу, о чему говори у првој књизи. Такође, први је уочио две гране хиперболе, о чему је, поред цртања тангенти хиперболе и изучавања њених асимптота, писао у другој књизи. У трећој књизи се бавио одабраним теоремама о површинама и хармонијским својствима полова коника. Четврта књига је била наставак треће, док су пета, шеста и седма његова сопствена открића. Најоригиналнијом од свих се сматра пета књига у којој се разматра нормала као максимална и минимална права линија повучена из тачке на криву. Књига шест говори о подударности и сличности конуса, док књига седам говори о пречницима и праволинијским фигурама описаним над тим пречницима. Аполоније је био и први који је дао имена: "парабола", "хипербола" и "елипса". Иако му није био познат алгебарски начин представљања коника, многи Аполионијеви резултати се могу непосредно записати методом координата. Сматра се једним од највећих математичара који су се бавили геометријом у историји, а највећим у старој Грчкој, поред Еуклида.
Последњи антички великан геометрије који је проучавао кусне пресеке био је Папо (Pappus, 290—350. године нове ере) из Александрије. У свом делу "Колекција", поред тога што је објединио сазнања својих претходника, увео је и појмове фокуса и директрисе хиперболе.
Конусни пресеци у арапском свету уреди
Персијски математичар, физичар и астроном Ал-Кухи (Abū Sahl Wayjan ibn Rustam al-Qūhī) је у десетом веку направио инструмент за цртање конусних пресека. Инструмент се називао конусни компас. Користећи конике, тачније пресек две параболе, Ал-Кухи је решио проблем конструкције јенакостраничног петоугла уписаног у задати квадрат. Други персијски математичар Омар Ал-Хајам (Ghiyāth ad-Dīn Abu'l-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyām Nīshāpūrī, 1048—1131. године), који је такође био и астроном, филозоф, поета и полиглота, превео је Аполонијева дела на арапски језик. То су књиге пет, шест и седам Аполонијевог дела "Конусни пресеци". Такође, користио је параболу и (правоуглу) хиперболу при решавању кубних једначина.
Европа уреди
У Европи се научници дуго нису бавили коникама, све до доба Ренесансе. Први значајни помак су били Кеплерови закони (Johannes Kepler, 1571—1630). Кеплер, немачки астроном је поставио три теорије познате као "Кеплерови закони". Први Кеплеров закон је најзначајнији за наставак изучавања коника и говори о томе да се тела Сунчевог система крећу око Сунца по коници, а да се само Сунце налази у жижи те конике. Он је разликовао пет врста коника, за разлику од Аполонија који је разликовао само три врсте. Конике које је Кеплер разликовао су кружница, елипса, парабола, хипербола и права. Сматра се да је и први у Европи увео називе "фокус" и "директриса" 1604. године (први их је увео Папо, везане за хиперболу у старој Грчкој). Сматра се да је тврдио да се померањем фокуса једне конике може добити друга (од елипсе се може добити круг приближавањем жижа, док се њиховим удаљавањем може добити парабола). Први је почео да изучава закон континуитета. Ослањајући се на Кеплерове радове, касније је његово изучавање наставио Готфрид Лајбниц Gottfried Wilhelm Leibniz.
Проучавање коника је нарочито било убрзано настанком пројективне геометрије чији су утемељивачи били Дезарг (Girard Desargues, 1591—1661), Лаир (Philippe de La Hire, 1640—1718.) и Паскал (Blaise Pascal, 1623—1662). Једно од познатијих Паскалових дела је "Теорема о мистичном хексаграму" у коме се налази и доказ теореме: "Уколико је у конику уписан хексаграм 1231'2'3', онда су пресеци три пара супротних страница 12' са 1'2, 23' са 2'3 и 13'са 1'3 колинеарни".
Рене Декарт (René Descartes, 1596—1650.) је заједно са Пјером Фермаом (Pierre de Fermat, 1601—1665.) поставио темеље данашње аналитичке геометрије. Они су сводили геометријске проблеме коника на алгебарске проблеме и на тај начин их решавали. Џон Волис (John Wallis, 1616—1703.) је први, 1655. године дефинисао конике као случајеве једначина другог степена. Ипак, можда и највећи значај коникама и конусним пресецима је дао Исак Њутн (Sir Isaac Newton, 1642—1726/27.) открићем да су орбите небеских тела конике, односно доказивањем Кеплерових закона. Данас, кружни зупчаници покрећу машине, такође знамо за параболичне тањирасте антене и фарове аутомобила, док цистерне и ехо локатори користе особине хипербола, односно, конике су свуда око нас.
Особине конусних пресека уреди
За све конике, осим круга, важи да постоји тачка која се назива жижа конике, и права која се назива директриса такве да је однос растојања произвољне тачке конике до жиже ' и директрисе константан.
Тај однос се назива ексцентритетом конике и означава са . Уколико је ексцентрицитет између 0 и 1, коника је елипса, а у специјалном случају, када је ексцентрицитет једнак 0, коника је круг. Парабола има ексцентрицитет 1, док је коника чији је ексцентрицитет већи од 1 хипербола.
Теорема. Свака коника, осим круга, је геометријско место тачака у равни за које је однос растојања од неке тачке (жижа) и неке сталне праве (директриса) константна величина.
Жижа круга је уједно и његов центар, а директирса је бесконачно далека права. Елипса и хипербола имају две жиже и одговарајуће директрисе. Парабола има само једну жижу и једну директрису.
Још једна особина заједничка за све конике, осим параболе, је линеарни ексцентрицитет. Линеарни ексцентрицитет представља удаљенсост центра конике до њене жиже, или једне од жижа. Најчешће се означава са .
Тетива која пролази кроз жижу или једну од две жиже конике и паралелна је директриси се назива latus rectum. Жижни (фокусни) параметар конике је растојање између жиже, или једне од жижа конике, и директрисе. Означава се са .
| коника | канонска једначина | ексцентрицитет ( ) | линеарни ексцентрицитет ( ) | latus rectum ( ) | фокусни параметар ( ) |
|---|---|---|---|---|---|
| круг | |||||
| елипса | |||||
| парабола | |||||
| хипербола |
Конструкција уреди
Три основна конусна пресека су елипса, парабола и хипербола. Кружница се може третирати као четврта коника, или као специјалан случај елипсе. Кружница и елипса се добијају када је пресек кружног конуса са равни затворена крива. Кружница се добија када се раван која сече конус постави парелелно са равни која генерише кружницу конуса - када је у питању прав конус као на слици на врху стране, пресечна раван нормална је на осу симетрије конуса. Уколико је пресечна раван паралелна тачно једној правој која генерише конус (изводници конуса), добијени конусни пресек није ограничен и назива се парабола. У преосталом случају, када раван пресеца обе компоненте конуса, добијају се две раздвојене неограничене криве које се називају гранама хиперболе.
Канонски облик уреди
У Декартовим координатама једначине коника се могу записати у свом канонском облику:[1]
- Кружница:
- Елипса:
- Парабола:
- Хипербола:
Парабола поседује својство осне симетрије, док су кружница, елипса и хипербола централно симетричне.
Конусни пресеци могу бити задати и својим параметарским једначинама:
Декартов координатни систем уреди
У Декартовом координатном систему, график квадратне функције две непознате може бити конусни пресек.
Једначина конусних пресека је облика: [2], где и нису сви једнаки нули.
Како скалирање константи и не утиче на скуп нула функције , конусни пресеци се могу посматрати као тачке у петодимензионом пројективном простору .
Класификација према дискриминанти уреди
Конусни пресеци дати овом једначином могу да се класификују према вредности дискриминанте[3] .
Ако конусни пресеци нису дегенерисани, тада:
- ако је , једначина представља елипсу
- ако је , једначина представља параболу
- ако је , једначина представља хиперболу
- ако је поред тога и , једначина представља правоугаону хиперболу
Како би разликовали дегенерисане случајеве од стандардних (недегенерисаних), нека је детерминанта 3х3 матрице:
, тј. .
Конусни пресек није дегенерисан ако и само ако је ∆ ≠ 0. Ако је ∆ = 0 у питању је неки од случајева дегенерисаних конусних пресека.
Матрична нотација уреди
Једначина конусног пресека може да се напише у матричом облику:
Тип конике је јединствено одређен детерминантом матрице у средини претходне једначине. Ако је детерминанта позитивна, нула или негативна, тада је у питању елипса, парабола или хипербола респективно. Ако су обе својствене вредности средње матрице различити од нуле (тј. ако коника елипса или хипербола), променљиве се могу трансформисати тако да се добија:
где a,c и G задовољавају и .
Такође се може записати у облику:
.
Ако је детерминанта средње матрице (3х3) различита од нуле, конусни пресек није дегенерисан. Ако је детерминанта једнака нули, конусни пресек је дегенерисана парабола (две паралелне или две праве које се поклапају), дегенерисана елипса (тачка елипсе), или дегенерисана хипербола (две праве које се секу).
Део квадратне форме уреди
Једначина
се може написати у следећем облику:
.
Дакле, конику можемо представити као пресек графика квадратне форме и равни .
Ексцентрицитет изражен преко параметара квадратне форме уреди
Када је коника записана алгебарски као:
,
ексцентрицитет се може записати као функција прараметара квадратне једначине.[4] Ако је , коника је парабола и њен ексцентрицитет је једнак 1. У супротном случају, узимајући у обзир да једначина представља хиперболу или неимагинарну елипсу, ексентрицитет је дат са:
где је ако је детерминанта матрице 3х3 (из матричне нотације) негативна, а ако је та детерминанта позитивна.
Инваријанте коника уреди
Траг и детерминанта су инваријанте у односу на ротацију око координатних оса и транслацију равни.[5][6]
Константан израз је инваријанта само приликом ротације.
Модификовани облик уреди
За неке практичне примене корисно је да се коника представи у поларном координатном систему, у облику у коме је тачка фокуса постављена у координатни почетак. Други фокус, ако постоји, поставља се на негативни део (код елипсе), односно позитивни део х-осе (код хиперболе). Та једначина има облик:
,
где је ексцентрицитет, а половина дужине сегментне линије која спаја две тачке конике и притом пролази кроз фокус и паралелна је директриси (latus rectum):
, где су и полуосе конике.
За имамо круг, за елипсу, за параболу и за хиперболу.
Поларни облик једначине конусних пресека се често користи у динамици; на пример, за одређивање орбита објеката који се крећу око Сунца.[7]
У Декартовом координатном систему једначина има облик:
Линеарни ексцентрицитет је дат са:
Из општих формула, различити конусни пресеци могу у Декартовим координатама бити представљени на следећи начин:
- Круг:
- Елипса:
- Парабола:
- Хипербола:
Пет тачака одређују конику уреди
Пет копланарних тачака, међу којима никоје три нису колинеарне, јединствено одређују конику. Уколико међу пет копланарних тачака постоје три или више колинеарних тачака, оне такође одређују конусни пресек, али један од три дегенерисана случаја.
Дегенерисани конусни пресеци уреди
Дегерисаним случајем сматрамо пресек равни и конуса који садржи теме конуса. То могу бити:
- тачка, када је угао између равни и осе конуса већи од угла између осе и изводнице конуса (и мањи од 180° – угао између осе и изводнице конуса);
- права, када је угао између равни и осе конуса исти као угао између осе и изводнице конуса;
- две праве које се секу, када је угао између равни и осе конуса мањи од угла између осе и изводнице конуса.
-
Тачка
-
Права
-
Две праве
Конике у другим областима уреди
Коси хитац уреди
Кретање тела које се испаљује са висине , са почетном брзином и под углом у односу на тло, коси хитац, а путања коју тело описује овим кретањем је парабола. Приметимо да, ако занемаримо отпор ваздуха, осим почетних услва, на тело ће деловати и гравитационо поље.
Кретања тела Сунчевог система уреди
Први Кеплеров закон каже да се тела Сунчевог система крећу око Сунца по коници у чијој се жижи налази Сунце. Већина планета се креће по приближно кружној путањи, зато што им је ексцентрицитет близак нули (Земљин 0.0167, а Јупитеров 0.0488). Интересантно је да Халејева комета има ексцентрицитет близак јединици (око 0.995).
Радио антене (у астрономији) уреди
Радио антене се ослањају на оптичка својства коника. Радио талас, због велике таласне дужине, није једноставно детектовати, па се због тога користе параболоидне антене, у чијој се жижи налази пријемник. Због великих удаљености сви зраци коју падну на површ су приближно паралелни и одбиће се тачно у пријемник (жижу параболоида).
-
Одбијање зракова од рефлектор
Елиптички сто за билијар уреди
Елиптички сто за билијар користи оптичка својства елипсе. Уколико би се извео ударац без спина са беле тачке, у било ком правцу, кугла би ушла у рупу. То својство стола се добија тиме што се тачка са које се изводи ударац и рупа налазе у жижама елипсе. Пример стола можете видети на видео клипу: Pool Table - Numberphile.[8]
Референце уреди
- ^ Protter & Morrey (1970). pp. 314—328, 585-589
- ^ Protter & Morrey (1970, 316. str)
- ^ Fanchi, John R. (2006), [1], John Wiley and Sons, pp. 44 i 45, [2]
- ^ Ayoub, Ayoub B., "The eccentricity of a conic section," [Ayoub, Ayoub B., "The eccentricity of a conic section,"] 34(2), Mart 2003, 116–121.
- ^ Protter & Morrey (1970). pp. 326
- ^ Pettofrezzo, Anthony, "Matrices and Transformations", Dover Publ., (1966). pp. 101–111
- ^ Brannan, Esplen & Gray 1999, стр. 17.
- ^ Elliptical Pool Table - Numberphile
Литература уреди
- Šukilović, T. Vukmirović, S.(2015), Geometrija za informatičare, Matematički fakultet u Beogradu
- Akopyan, A.V. & Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. ISBN 978-0-8218-4323-9.
- Boyer, Carl B. (2004) [1956]. History of Analytic Geometry. Dover. ISBN 978-0-486-43832-0.
- Dixon, A. C. (март 1908), „The Conic through Five Given Points”, The Mathematical Gazette, The Mathematical Association, JSTOR 3605147
Спољашње везе уреди
- Конусни пресеци на mathworld.wolfram.com (језик: енглески)
- Извођење једначина конусних пресека (језик: енглески)
- Конусни пресеци (језик: енглески)
- Појава коника у природи (језик: енглески)
- Конике (језик: енглески)
- Аналитичка геометрија равни[мртва веза]