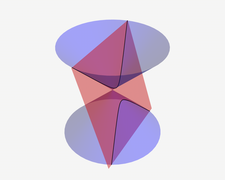
Konusni presek

Konusni preseci zauzimaju veoma značajno mesto kako u geometriji, tako i u celoj matematici. Konusni presek predstavlja presek konusa i proizvoljne ravni u prostoru. Postoje različiti slučajevi preseka. Dele se na degenerisane (tačka, prava ili dve prave koje se seku), i nedegenerisane (krive). Nedegenerisani su preseci kod kojih ravan ne sadrži teme konusa i takvi preseci se nazivaju konike. Tu spadaju parabola, hiperbola, elipsa, kao i specijalni slučaj elipse - krug. Osnovna karakteristika nedegenerisanih konusnih preseka (osim kruga) je da postoje tačka (žiža) i prava (direktrisa) takve da je odnos rastojanja proizvoljne tačke konike do njih konstantan. U analitičkoj geometriji, konika se može definisati kao ravanska algebarska kriva drugog reda. Takođe, konike su veoma značajne za mnoge oblasti. Na primer, u astronomiji: nebeska tela se kreću putanjama koje su zapravo konike, u optici (konstrukcija sočiva i ogledala), mehanici i mnogim drugim oblastima. Često se primenjuju i u paleontologiji za razumevanje izgleda određenih organizama.

• 
  Elipsa
• 
  Krug
• 
  Hiperbola
• 
  Parabola

Istorija konusnih preseka

Stara Grčka

Proučavanje konusnih preseka datira još od vremena starih Grka. Smatra se da je prvi koji je otkrio, definisao i opisao konusne preseke bio Menehmo (Menaechmus, oko 375—325. godine pre nove ere), Platonov učenik i tutor Aleksandra Velikog. Mehnemov rad nije sačuvan tako da danas o njemu saznajemo samo iz različitih spisa njegovih savremenika. Koristio je konusne preseke u pokušaju rešavanja tri problema konstruktivne geometrije: kvadrature kruge, trisekcije ugla i udvostručavanja kocke. Definicija koja se tada koristila se razlikuje od ove današnje. Tek kada je u 19. veku dokazano da navedena tri problema nisu rešiva upotrebom samo lenjira i šestara, konusni preseci su počeli da se definišu kao preseci uspravnog kružnog konusa i ravni. U staroj Grčkoj su konuse konstruisali obrtanjem pravouglog trougla oko jedne od kateta, tako da hipotenuza generiše površinu konusa. Konusni preseci su se dobijali konstruisanjem ravni koja je presecala konus. Određivanje konike se vršilo tako što se posmatrao ugao između ravni i temenog ugla (dvostruke veličine ugla koji obrazuju hipotenuza i kateta oko koje se rotira trougao). Ukoliko je taj ugao oštar, konika je elipsa, ako je prav, parabola, i ukoliko je ugao tup, u pitanju je hiperbola. Smatra se da se konusnim presecima bavio i Euklid (Euclid, oko 330—275. godine pre nove ere), međutim ni njegovi radovi nisu sačuvani. Konike, sa posebnim akcentom na parabolu, proučavao je i Arhimed (Archimedes, 287—212. godine pre nove ere). Njegovi radovi poput "Rasprave o kvadraturi parabole" su sačuvani do danas.

U proučavanju konika poseban doprinos je dao Apolonije (Appollonius, oko 262—190. godine pre nove ere), grčki matematičar i astronom. On je napisao monografiju "Konusni preseci" koja se sastojala od osam knjiga sa 787 stavova. Prve četiri knjige su na grčkom jeziku, naredne tri na persijskom, dok je osma, poslednja, izgubljena. Apolonije je prvi koji je dao osnovne teorije o sve tri konike na kružnom, uspravnom ili kosom konusu, o čemu govori u prvoj knjizi. Takođe, prvi je uočio dve grane hiperbole, o čemu je, pored crtanja tangenti hiperbole i izučavanja njenih asimptota, pisao u drugoj knjizi. U trećoj knjizi se bavio odabranim teoremama o površinama i harmonijskim svojstvima polova konika. Četvrta knjiga je bila nastavak treće, dok su peta, šesta i sedma njegova sopstvena otkrića. Najoriginalnijom od svih se smatra peta knjiga u kojoj se razmatra normala kao maksimalna i minimalna prava linija povučena iz tačke na krivu. Knjiga šest govori o podudarnosti i sličnosti konusa, dok knjiga sedam govori o prečnicima i pravolinijskim figurama opisanim nad tim prečnicima. Apolonije je bio i prvi koji je dao imena: "parabola", "hiperbola" i "elipsa". Iako mu nije bio poznat algebarski način predstavljanja konika, mnogi Apolionijevi rezultati se mogu neposredno zapisati metodom koordinata. Smatra se jednim od najvećih matematičara koji su se bavili geometrijom u istoriji, a najvećim u staroj Grčkoj, pored Euklida.

Poslednji antički velikan geometrije koji je proučavao kusne preseke bio je Papo (Pappus, 290—350. godine nove ere) iz Aleksandrije. U svom delu "Kolekcija", pored toga što je objedinio saznanja svojih prethodnika, uveo je i pojmove fokusa i direktrise hiperbole.

Konusni preseci u arapskom svetu

Dijagram Apolonijevih konika, 9. vek, arapski prevod

Persijski matematičar, fizičar i astronom Al-Kuhi (Abū Sahl Wayjan ibn Rustam al-Qūhī) je u desetom veku napravio instrument za crtanje konusnih preseka. Instrument se nazivao konusni kompas. Koristeći konike, tačnije presek dve parabole, Al-Kuhi je rešio problem konstrukcije jenakostraničnog petougla upisanog u zadati kvadrat. Drugi persijski matematičar Omar Al-Hajam (Ghiyāth ad-Dīn Abu'l-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyām Nīshāpūrī, 1048—1131. godine), koji je takođe bio i astronom, filozof, poeta i poliglota, preveo je Apolonijeva dela na arapski jezik. To su knjige pet, šest i sedam Apolonijevog dela "Konusni preseci". Takođe, koristio je parabolu i (pravouglu) hiperbolu pri rešavanju kubnih jednačina.

Evropa

U Evropi se naučnici dugo nisu bavili konikama, sve do doba Renesanse. Prvi značajni pomak su bili Keplerovi zakoni (Johannes Kepler, 1571—1630). Kepler, nemački astronom je postavio tri teorije poznate kao "Keplerovi zakoni". Prvi Keplerov zakon je najznačajniji za nastavak izučavanja konika i govori o tome da se tela Sunčevog sistema kreću oko Sunca po konici, a da se samo Sunce nalazi u žiži te konike. On je razlikovao pet vrsta konika, za razliku od Apolonija koji je razlikovao samo tri vrste. Konike koje je Kepler razlikovao su kružnica, elipsa, parabola, hiperbola i prava. Smatra se da je i prvi u Evropi uveo nazive "fokus" i "direktrisa" 1604. godine (prvi ih je uveo Papo, vezane za hiperbolu u staroj Grčkoj). Smatra se da je tvrdio da se pomeranjem fokusa jedne konike može dobiti druga (od elipse se može dobiti krug približavanjem žiža, dok se njihovim udaljavanjem može dobiti parabola). Prvi je počeo da izučava zakon kontinuiteta. Oslanjajući se na Keplerove radove, kasnije je njegovo izučavanje nastavio Gotfrid Lajbnic Gottfried Wilhelm Leibniz.

Proučavanje konika je naročito bilo ubrzano nastankom projektivne geometrije čiji su utemeljivači bili Dezarg (Girard Desargues, 1591—1661), Lair (Philippe de La Hire, 1640—1718.) i Paskal (Blaise Pascal, 1623—1662). Jedno od poznatijih Paskalovih dela je "Teorema o mističnom heksagramu" u kome se nalazi i dokaz teoreme: "Ukoliko je u koniku upisan heksagram 1231'2'3', onda su preseci tri para suprotnih stranica 12' sa 1'2, 23' sa 2'3 i 13'sa 1'3 kolinearni".

Rene Dekart (René Descartes, 1596—1650.) je zajedno sa Pjerom Fermaom (Pierre de Fermat, 1601—1665.) postavio temelje današnje analitičke geometrije. Oni su svodili geometrijske probleme konika na algebarske probleme i na taj način ih rešavali. Džon Volis (John Wallis, 1616—1703.) je prvi, 1655. godine definisao konike kao slučajeve jednačina drugog stepena. Ipak, možda i najveći značaj konikama i konusnim presecima je dao Isak Njutn (Sir Isaac Newton, 1642—1726/27.) otkrićem da su orbite nebeskih tela konike, odnosno dokazivanjem Keplerovih zakona. Danas, kružni zupčanici pokreću mašine, takođe znamo za parabolične tanjiraste antene i farove automobila, dok cisterne i eho lokatori koriste osobine hiperbola, odnosno, konike su svuda oko nas.

Osobine konusnih preseka

Za sve konike, osim kruga, važi da postoji tačka $F$ koja se naziva žiža konike, i prava $d$ koja se naziva direktrisa takve da je odnos rastojanja proizvoljne tačke $M$ konike do žiže $F$' i direktrise $d$ konstantan.

$e={\frac {MF}{d(M,d)}}$

Taj odnos se naziva ekscentritetom konike i označava sa $e$. Ukoliko je ekscentricitet između 0 i 1, konika je elipsa, a u specijalnom slučaju, kada je ekscentricitet jednak 0, konika je krug. Parabola ima ekscentricitet 1, dok je konika čiji je ekscentricitet veći od 1 hiperbola.

Teorema. Svaka konika, osim kruga, je geometrijsko mesto tačaka u ravni za koje je odnos rastojanja od neke tačke $F$ (žiža) i neke stalne prave $d$ (direktrisa) konstantna veličina.

Žiža kruga je ujedno i njegov centar, a direktirsa je beskonačno daleka prava. Elipsa i hiperbola imaju dve žiže i odgovarajuće direktrise. Parabola ima samo jednu žižu i jednu direktrisu.

Još jedna osobina zajednička za sve konike, osim parabole, je linearni ekscentricitet. Linearni ekscentricitet predstavlja udaljensost centra konike do njene žiže, ili jedne od žiža. Najčešće se označava sa $c$.

Tetiva koja prolazi kroz žižu ili jednu od dve žiže konike i paralelna je direktrisi se naziva latus rectum. Žižni (fokusni) parametar konike je rastojanje između žiže, ili jedne od žiža konike, i direktrise. Označava se sa $p$.

konika	kanonska jednačina	ekscentricitet ($e$)	linearni ekscentricitet ($c$)	latus rectum ($l$)	fokusni parametar ($p$)
krug	${x^{2}}+{y^{2}}=r^{2},\ r>0$	$0$	$0$	$r$	$\infty$
elipsa	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,\ a>b>0$	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {{a^{2}}-{b^{2}}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {{a^{2}}-{b^{2}}}}}$
parabola	$y^{2}=2px,\ p>0$	$1$	$-$	$2a$	$2a$
hiperbola	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\ a,b>0$	${\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {{a^{2}}+{b^{2}}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {{a^{2}}+{b^{2}}}}}$

Konstrukcija

Tri osnovna konusna preseka su elipsa, parabola i hiperbola. Kružnica se može tretirati kao četvrta konika, ili kao specijalan slučaj elipse. Kružnica i elipsa se dobijaju kada je presek kružnog konusa sa ravni zatvorena kriva. Kružnica se dobija kada se ravan koja seče konus postavi parelelno sa ravni koja generiše kružnicu konusa - kada je u pitanju prav konus kao na slici na vrhu strane, presečna ravan normalna je na osu simetrije konusa. Ukoliko je presečna ravan paralelna tačno jednoj pravoj koja generiše konus (izvodnici konusa), dobijeni konusni presek nije ograničen i naziva se parabola. U preostalom slučaju, kada ravan preseca obe komponente konusa, dobijaju se dve razdvojene neograničene krive koje se nazivaju granama hiperbole.

Kanonski oblik

U Dekartovim koordinatama jednačine konika se mogu zapisati u svom kanonskom obliku:

• Kružnica: $x^{2}+y^{2}=r^{2}\,$
• Elipsa: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1$
• Parabola: $y^{2}=2px$
• Hiperbola: ${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1,\;{x^{2} \over b^{2}}-{y^{2} \over a^{2}}=-1$

Parabola poseduje svojstvo osne simetrije, dok su kružnica, elipsa i hiperbola centralno simetrične.

Konusni preseci mogu biti zadati i svojim parametarskim jednačinama:

• Kružnica: $(x=x_{0}+rcos\theta ,\ y=y_{0}+rsin\theta ),\qquad \theta \in [0,2\pi )$,
• Elipsa: $(x=x_{0}+acos\theta ,\ y=y_{0}+bsin\theta ),\qquad \theta \in [0,2\pi )$,
• Parabola: $(x=x_{0}+{\frac {t^{2}}{2p}},\ y=y_{0}+t),\qquad t\in R$,
• Hiperbola: $x=x_{0}\pm a\cosh \theta ,\ y=y_{0}+b\sinh \theta ),\qquad \theta \in R$.

Dekartov koordinatni sistem

U Dekartovom koordinatnom sistemu, grafik kvadratne funkcije dve nepoznate $f(x,y)$ može biti konusni presek.

Jednačina konusnih preseka je oblika: $f(x,y)\equiv Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$, gde $A,B,C,D,E$ i $F$ nisu svi jednaki nuli.

Kako skaliranje konstanti $A,B,C,D,E$ i $F$ ne utiče na skup nula funkcije $f(x,y)$, konusni preseci se mogu posmatrati kao tačke u petodimenzionom projektivnom prostoru $P^{5}$.

Klasifikacija prema diskriminanti

Konusni preseci dati ovom jednačinom mogu da se klasifikuju prema vrednosti diskriminante $B^{2}-4AC$.

Ako konusni preseci nisu degenerisani, tada:

• ako je $B^{2}-4AC<0$, jednačina predstavlja elipsu
  • ako je $A=C$ i $B=0$, jednačina predstavlja krug, koji je specijalni slučaj elipse
• ako je $B^{2}-4AC=0$, jednačina predstavlja parabolu
• ako je $B^{2}-4AC>0$, jednačina predstavlja hiperbolu
  • ako je pored toga i $A+C=0$, jednačina predstavlja pravougaonu hiperbolu

Kako bi razlikovali degenerisane slučajeve od standardnih (nedegenerisanih), neka je $\Delta$ determinanta 3h3 matrice:

${\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}$, tj. $\Delta =(AC-B^{2}/4)F+BED/4-CD^{2}/4-AE^{2}/4$.

Konusni presek nije degenerisan ako i samo ako je ∆ ≠ 0. Ako je ∆ = 0 u pitanju je neki od slučajeva degenerisanih konusnih preseka.

Matrična notacija

Jednačina konusnog preseka može da se napiše u matričom obliku:

${\begin{bmatrix}x&y\end{bmatrix}}{\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+Dx+Ey+F=0$

Tip konike je jedinstveno određen determinantom matrice u sredini prethodne jednačine. Ako je determinanta pozitivna, nula ili negativna, tada je u pitanju elipsa, parabola ili hiperbola respektivno. Ako su obe svojstvene vrednosti srednje matrice različiti od nule (tj. ako konika elipsa ili hiperbola), promenljive se mogu transformisati tako da se dobija:

$\left({\begin{array}{c}x-a\\y-c\end{array}}\right)^{T}\left({\begin{array}{cc}A&{\frac {B}{2}}\\{\frac {B}{2}}&C\end{array}}\right)\left({\begin{array}{c}x-a\\y-c\end{array}}\right)=G$

gde a,c i G zadovoljavaju $D+2aA+Bc=0,E+2Cc+Ba=0$ i $G=Aa^{2}+Cc^{2}+Bac-F$.

Takođe se može zapisati u obliku:

${\begin{bmatrix}x&y&1\end{bmatrix}}{\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}=0$.

Ako je determinanta srednje matrice (3h3) različita od nule, konusni presek nije degenerisan. Ako je determinanta jednaka nuli, konusni presek je degenerisana parabola (dve paralelne ili dve prave koje se poklapaju), degenerisana elipsa (tačka elipse), ili degenerisana hiperbola (dve prave koje se seku).

Deo kvadratne forme

Jednačina

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

se može napisati u sledećem obliku:

$Ax^{2}+Bxy+Cy^{2}=-(Dx+Ey+F)$.

Dakle, koniku možemo predstaviti kao presek grafika kvadratne forme $z=Ax^{2}+Bxy+Cy^{2}$ i ravni $z=-(Dx+Ey+F)$.

Ekscentricitet izražen preko parametara kvadratne forme

Kada je konika zapisana algebarski kao:
$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$,
ekscentricitet se može zapisati kao funkcija prarametara kvadratne jednačine. Ako je $4AC=B^{2}$, konika je parabola i njen ekscentricitet je jednak 1. U suprotnom slučaju, uzimajući u obzir da jednačina predstavlja hiperbolu ili neimaginarnu elipsu, eksentricitet je dat sa:

$e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}}$

gde je $\eta =1$ ako je determinanta matrice 3h3 (iz matrične notacije) negativna, a $\eta =-1$ ako je ta determinanta pozitivna.

Invarijante konika

Trag i determinanta ${\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}$ su invarijante u odnosu na rotaciju oko koordinatnih osa i translaciju ravni.

Konstantan izraz $F$ je invarijanta samo prilikom rotacije.

Modifikovani oblik

Za neke praktične primene korisno je da se konika predstavi u polarnom koordinatnom sistemu, u obliku u kome je tačka fokusa postavljena u koordinatni početak. Drugi fokus, ako postoji, postavlja se na negativni deo (kod elipse), odnosno pozitivni deo h-ose (kod hiperbole). Ta jednačina ima oblik:

$r={\frac {l}{1-e\cos {\theta }}}$,

gde je $e$ ekscentricitet, a $l$ polovina dužine segmentne linije koja spaja dve tačke konike i pritom prolazi kroz fokus i paralelna je direktrisi (latus rectum):

$l={\frac {b^{2}}{a}}$, gde su $a$ i $b$ poluose konike.

Za $e=0$ imamo krug, za $0<e<1$ elipsu, za $e=1$ parabolu i za $e>1$ hiperbolu.

Polarni oblik jednačine konusnih preseka se često koristi u dinamici; na primer, za određivanje orbita objekata koji se kreću oko Sunca.

U Dekartovom koordinatnom sistemu jednačina ima oblik:

${\begin{alignedat}{7}{\sqrt {x^{2}+y^{2}}}=\left(l+ex\right)\ \Rightarrow \ \left({\frac {x-{\frac {le}{1-e^{2}}}}{\frac {l}{1-e^{2}}}}\right)^{2}+{\frac {\left(1-e^{2}\right)y^{2}}{l^{2}}}=1\end{alignedat}}$

Linearni ekscentricitet je dat sa:

$c=\left({\frac {le}{1-e^{2}}}\right)$

Iz opštih formula, različiti konusni preseci mogu u Dekartovim koordinatama biti predstavljeni na sledeći način:

• Krug: $x^{2}+y^{2}=r^{2}$
• Elipsa: ${\frac {(x-{\sqrt {a^{2}-b^{2}}})^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
• Parabola: $y^{2}=4a(x+a)$
• Hiperbola: ${\frac {(x+{\sqrt {a^{2}+b^{2}}})^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Pet tačaka određuju koniku

Pet koplanarnih tačaka, među kojima nikoje tri nisu kolinearne, jedinstveno određuju koniku. Ukoliko među pet koplanarnih tačaka postoje tri ili više kolinearnih tačaka, one takođe određuju konusni presek, ali jedan od tri degenerisana slučaja.

Konstrukcija konike pomoću pet tačaka.

Degenerisani konusni preseci

Degerisanim slučajem smatramo presek ravni i konusa koji sadrži teme konusa. To mogu biti:

• tačka, kada je ugao između ravni i ose konusa veći od ugla između ose i izvodnice konusa (i manji od 180° – ugao između ose i izvodnice konusa);
• prava, kada je ugao između ravni i ose konusa isti kao ugao između ose i izvodnice konusa;
• dve prave koje se seku, kada je ugao između ravni i ose konusa manji od ugla između ose i izvodnice konusa.

• 
  Tačka
• 
  Prava
• 
  Dve prave

Konike u drugim oblastima

Kosi hitac

Kretanje tela koje se ispaljuje sa visine $h$, sa početnom brzinom ${\vec {v}}_{0}$ i pod uglom $\alpha$ u odnosu na tlo, kosi hitac, a putanja koju telo opisuje ovim kretanjem je parabola. Primetimo da, ako zanemarimo otpor vazduha, osim početnih uslva, na telo će delovati i gravitaciono polje.

Kretanja tela Sunčevog sistema

Prvi Keplerov zakon kaže da se tela Sunčevog sistema kreću oko Sunca po konici u čijoj se žiži nalazi Sunce. Većina planeta se kreće po približno kružnoj putanji, zato što im je ekscentricitet blizak nuli (Zemljin 0.0167, a Jupiterov 0.0488). Interesantno je da Halejeva kometa ima ekscentricitet blizak jedinici (oko 0.995).

Radio antene (u astronomiji)

Radio antene se oslanjaju na optička svojstva konika. Radio talas, zbog velike talasne dužine, nije jednostavno detektovati, pa se zbog toga koriste paraboloidne antene, u čijoj se žiži nalazi prijemnik. Zbog velikih udaljenosti svi zraci koju padnu na površ su približno paralelni i odbiće se tačno u prijemnik (žižu paraboloida).

• 
  Very Large Array
• 
  Odbijanje zrakova od reflektor

Eliptički sto za bilijar

Eliptički sto za bilijar koristi optička svojstva elipse. Ukoliko bi se izveo udarac bez spina sa bele tačke, u bilo kom pravcu, kugla bi ušla u rupu. To svojstvo stola se dobija time što se tačka sa koje se izvodi udarac i rupa nalaze u žižama elipse. Primer stola možete videti na video klipu: Pool Table - Numberphile.

Eliptički sto za bilijar

Literatura

• Šukilović, T. Vukmirović, S.(2015), Geometrija za informatičare, Matematički fakultet u Beogradu CS1 održavanje: Višestruka imena: spisak autora (veza)
• Akopyan, A.V. & Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. ISBN 978-0-8218-4323-9. 
• Boyer, Carl B. (2004) [1956]. History of Analytic Geometry. Dover. ISBN 978-0-486-43832-0. 
• Dixon, A. C. (mart 1908), „The Conic through Five Given Points”, The Mathematical Gazette, The Mathematical Association, JSTOR 3605147 

Spoljašnje veze

• Konusni preseci na mathworld.wolfram.com (jezik: engleski)
• Izvođenje jednačina konusnih preseka (jezik: engleski)
• Konusni preseci (jezik: engleski)
• Pojava konika u prirodi (jezik: engleski)
• Konike (jezik: engleski)
• Analitička geometrija ravni