Стехиометрија
Стехиометријски односи су квантитативни односи који следе из хемијских формула или хемијских једначина. У складу са тим сва израчунавања у вези са хемијским формулама или једначинама називају се стехиометријски односи (стехиометрија).[1] Стехиометрија је утемељена на закону одржања масе, где је укупна маса реагенаса једнака укупној маси производа. То значи да се односи између количине реагенаса и производа обично понашају као односи позитивних целих бројева. То истовремено говори да ако су познати износи одвојених реагенаса, онда се може израчунати и износ производа. Сагласно томе, ако је позната количина једног реагенса и количина производа, емпиријски се може одредити један од реагенаса, а затим се може израчунати и износ других реагенаса.[2][3][4][5]
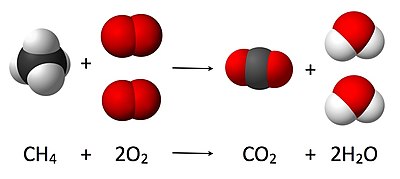
Ови односи се могу приказати уравнотеженом једначином:
- CH
4 + 2 O
2 → CO
2 + 2 H
2O.
Овде један молекул метана реагује са два молекула гасовитог кисеоника, па настају један молекул угљен диоксида и два молекула воде. Стехиометрија мери ове количинске односе, а користи се за одређивање количине производа/реагенаса који су производени/потребни у датој реакцији. Описани количински односи међу супстанцама у хемијској реакцији познати су као реакцијска стехиометрија. У горњем примеру, реакцијска стехиометрија мери однос између метана и кисеоника који у међусобној реакцији стварају угљен диоксид и воду.
Због познатог односа молске и атомске тежине, добијени стехиометријски коефицијенти могу се користити за одређивање тежине у реакцији која је описана у уравнотеженој једначини. То се зове композицијска стехиометрија.
Гасна стехиометрија бави се реакцијама које укључују гасове, а на основу познате температуре, притиска и запремине може се претпоставити да ли је дати узорак идеалан гас. За гасове, однос запремина је идеално исти као и онај по закону о идеалном гасу, али се однос масе једне реакције мора израчунати из молекулских маса реагенаса и производа. У пракси, због постојања изотопа, користе се моларне масе, уместо да се израчунава однос маса.
Етимологија
уредиИзраз стехиометрија је први пут користио Јеремијас Бенјамин Рихтер 1792. године, када је објављен први том његове књиге под називом Стехиометрија или уметност мерења хемијских елемената (Stoichiometry or the Art of Measuring the Chemical Elements). Назив је изведен из грчких речи στοιχεῖον - stoicheion = елемент + μέτρον – metron = мера. У патристичком грчком, реч stoichiometria је користио патријарх Нићифор I Цариградски када се односио на број линијских тачака канонског Новог завета и неких од Апокрифа.
Дефиниција
уредиСтехиометријска количина или стехиометријске однос реагенаса је њихова најповољнија количина или однос, а под претпоставком да је реакција комплетна, потебно је знати да:
- сви реагенси се троше;
- нема недостатка реагенаса;
- не постоји вишак реагенса.[6]
Стехиометрија почива на основним законима који помажу боље разумевање односа у реакцијама као што су: закон одржања масе, закон одређених пропорција (односно, закон сталног састава), закон више пропорција и закон реципрочних пропорција. У принципу, у хемијским реакцијама се сједињују одређени односи хемикалија. Хемијске реакције не могу ни створити ни уништити материју, нити трансмутирати један хемијски елемент у други, а износ сваког елемента мора бити исти у целокупној реакцији. На пример, број атома одређеног елемента X на реактантској страни мора бити једнак броју атома тог елемента на страни производа, без обзира да ли су или не сви од тих атома заправо укључени у реакцију.
Хемијске реакције, као макроскопске јединице операција, састоје се од веома великиог броја елементарних реакција, где један молекул реагује с другом молекулом. Када молекул (или његова половина) реагује, настаје завршни скуп атома у производу, а однос између реагенаса у потпуној реакцији је у интегрисаном односу. Реакција може да троши више од једног молекула, а стехиометријски број се објашњава као позитиван број за производе (збирно) и негативан за потрошене реагенсе.[7]
Различити елементи имају различите атомске масе, а као збирови појединачних атома, молекули имају одређену моларну масу, која је мерена јединицом мола (6,02 × 1023 појединачних молекула, а назива се Авогадрова константа). По дефиницији, угљеник-12 има моларну масу од 12 g/mol. Тако се израчунава стехиометрија масе, где је број молекула потребних за сваки реагенс изражен у моловима и помножен са моларном масом сваког реагенса по молу реакције. Односи маса могу се израчунати дељењем сваког од њих и укупном масом целе реакције. Елементи у свом природном стању су смесе изотопа с различитом масом, чиме се показује да атомске масе, а тиме и моларне масе нису баш цели бројеви. На пример, уместо тачне пропорције 14:3, добије се 17,04 kg амонијака 14,01 kg азота и 3 × 1,01 kg водоника, јер природни азот садржи мале количине азот-15, а природни водоник садржи водоник-2 (деутеријум).
Стехиометријски реагенс је онај реагенс који се троши у реакцији, за разлику од каталитског реагенса, који се у укупној реакцији не троши, јер реагује у једном кораку, а затим се и обнавља у још једном.
Претварање грама у молове
уредиСтехиометрија се не користи само за уравнотежавање хемијске једначине, него и у претварању грама супстанце у молове или грама у милилитре. На пример, да би се пронашао износ NaCl (натријум хлорида) у 2,00 g супстанце, треба учинити следеће:
У горњем примеру, када је написан у делимичном облику, грами чине умножавајуċи појам, који је једнак величини 1 (g/g = 1) са резултирајућим износом у моловима (јединици која је потребна), као што је приказано у сљедећој једначини:
Моларна пропорција
уредиСтехиометрија се често користи за уравнотежавање хемијске једначине (стехиометријска реакција). На пример, два диатомска молекула гаса, водоника и кисеоника, могу се сјединити при чему се добије течна вода, у егзотермној реакцији, а према следећој једначини:
- 2 H
2 + O
2 → 2 H
2O
Стехиометријска реакција у горњој једначини описује да је однос водоника, кисеоника и молекула воде 2:1:2.
Моларни однос омогућава претварање између молова једне супстанце у молове другог. На пример, у реакцији:
- 2 CH
3OH + 3 O
2 → 2 CO
2 + 4 H
2O
Количина воде која се производи потрошњом 0,27 мола CH
3OH, добија се применом молског односа између CH
3OH и H
2O од 2 до 4.
Назив стехиометрија се такође често користи за моларне пропорције елемената у стехиометријском једињењу (композицијска стехиометрија). На пример, стехиометрија водоника и кисеоника у H2O је 2:1. У стехиометријском једињењу, моларне пропорције су цели бројеви.
Одређивање износа производа
уредиСтехиометрија се такође може употребити за проналажење количине производа реакција. Ако се комад чврстог бакра (Cu) дода у водени раствор сребро нитрата (AgNO3), у реакцији једноструког премештања, стварају се водени бакар(II) нитрат (Cu(NO3)2) и чврсто сребро (Ag). Колико се добије сребра, ако се 16,00 грама Цу дода у раствор, за појаву вишка сребреног нитрата? У тражењу одговора се примењују следећи кораци:
- Написати и уравнотежити једначину;
- Изразити масу у молима: претварањем грама Cu у молове Cu;
- Наћи молни однос: претварањем молова Cu у молове произведеног Ag;
- Одредити молове у маси: претварањем молова Ag у граме произведеног Ag.
Потпуно уравнотежена једначина је:
- Cu + 2 AgNO
3 → Cu(NO
3)
2 + 2 Ag
У кораку маса-мол, маса бакра (16,00 g) се претвара у молове бакра дељењем масе бакра његовом молекулском масом: 63,55 g/mol.
Затим се, преко износа Cu у моловима (0,2518), тражи молски однос. То се изражава као коефицијент у балансираној реакцији: Cu и Ag су у односу 1:2.
Сада, када је позната количина произведеног Ag = 0,5036 mol, овај износ се претвара у граме произведеног Ag и долази се до коначног одговора:
Овај скуп прорачуна може се даље сажети у једноструки корак:
Остали примери
уредиЗа пропанску (C3H8) реакцију са гасовитим кисеоником (O2), уравнотежена хемијска једначина је:
- C
3H
8 + 5 O
2 → 3 CO
2 + 4 H
2O
Маса воде се добије ако 120 g пропана (C3H8) изгори у вишку кисика, тј. тада:
- .
Стехиометријски однос
уредиСтехиометрија се користи и за проналажење правог износу једног реагенса да „потпуно” реагује с другим реагенсом у хемијској реакцији, тј. стехиометријске количине ћији остаци реагенаса ċе се потрошити када се реакција одвије. Један пример је приказан испод, користећи реакцију стварања легуре жељезо – алуминијум:
- Fe
2O
3 + 2 Al → Al
2O
3 + 2 Fe
Ова једначина показује да ће 1 мол гвожђе(III) оксида и 2 мола алуминијума произвести 1 мол алуминијум оксида и 2 мола жељеза. Тако, за комплетну реакцију 85,0 g гвожђе(III)-оксида (0,532 мола), потребно 28,7 g (1,06 мола) алуминијума.
- .
Различите стехиометрије у конкурентским реакцијама
уредиЧесто је могуће више од једне реакције са истим почетним материјалима. Реакције се могу разликовати по својој стехиометрији. На пример, метилација бензена (C
6H
6), кроз Фридел-Крафтсове реакције користећи AlCl
3 као катализатор, може произвести једноструко метиловани (C
6H
5CH
3), двоструко метиловани (C
6H
4(CH
3)
2), или још више метиловане C
6H
6-n(CH
3)
n) производе, као што је приказано у следећем примеру,
- C
6H
6 + CH
3Cl → C
6H
5CH
3 + HCl - C
6H
6 + 2 CH
3Cl → C
6H
4(CH
3)
2 + 2 HCl - C
6H
6 + n CH
3Cl → C
6H
6-n(CH
3)
n + n HCl
У овом примеру, која реакција се одвија је делимично контролисана релативним концентрацијама реактаната.
Референце
уреди- ^ 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. „IUPAC. Compendium of Chemical Terminology”. doi:10.1351/goldbook.. Entry: "stoichiometric number".
- ^ Simpson, Michael G. (2011). Plant Systematics. Academic Press. ISBN 0-08-051404-9. Приступљено 12. 2. 2014.
- ^ Campbell N. A.; et al. (2008). Biology. 8th Ed. Person International Edition, San Francisco. ISBN 978-0-321-53616-7.
- ^ Alberts B.; et al. (2002). Molecular Biology of the Cell, 4th Ed. Garland Science. ISBN 0-8153-4072-9.
- ^ Voet D., Voet J. G. Biochemistry, 3rd Ed.[publisher= Wiley. ISBN 978-0-471-19350-0.
- ^ Carmen J. Giunta Journal of Chemical Education 2016 93 (4), 583-586 „What’s in a Name? Amount of Substance, Chemical Amount, and Stoichiometric Amount”. doi:10.1021/acs.jchemed.5b00690.
- ^ „stoichiometric number,”. iupac.org.
Литература
уреди- Ilya Prigogine; R. Defay (1954). Chemical Thermodynamics. translated by D.H. Everett; Chapter IV. Longmans, Green & Co. Exceptionally clear on the logical foundations as applied to chemistry; includes non-equilibrium thermodynamics.
- Ilya Prigogine (1967). Thermodynamics of Irreversible Processes, 3rd ed. Interscience: John Wiley & Sons. A simple, concise monograph. Library of Congress Catalog No. 67-29540
- E.A. Guggenheim (1967). Thermodynamics: An Advanced Treatment for Chemists and Physicists, 5th ed. North Holland; John Wiley & Sons (Interscience). A remarkably astute treatise. Library of Congress Catalog No. 67-20003
- Zumdahl, Steven S. Chemical Principles. Houghton Mifflin, New York, 2005, pp 148-150.
- Internal Combustion Engine Fundamentals, John B. Heywood
Спољашње везе
уреди- Engine Combustion primer from the University of Plymouth
- Free Stoichiometry Tutorials from Carnegie Mellon's ChemCollective
- Stoichiometry Add-In for Microsoft Excel Архивирано на сајту Wayback Machine (11. мај 2011) for calculation of molecular weights, reaction coëfficients and stoichiometry.
- Reaction Stoichiometry Calculator a comprehensive free online reaction stoichiometry calculator.
- Stoichiometry Plus a stoichiometry calculator and more for Android.