Наука о чврстоћи

Наука о чврстоћи је грана механике која проучава чврстоћу, крутост и стабилност конструкција и машина, те једноставних конструкцијских целина. Чврстоћа конструкције је способност преношења сила и оптерећења без лома материјала, трајних пластичних деформација или оштећења (пукотина). Крутост конструкције је отпорност конструкције према деформирању. Еластична стабилност конструкције је способност конструкције да задржи почетан равнотежни облик. Губитак еластичне стабилности назива се извијање.

Силнице унутрашњих сила су гушће у близини рупе (уобичајени распоред напрезања).

Греда је издужена водоравна или коса носива грађевна конструкција за преношење вертикалних оптерећења на лежаје, ослоњена на својим крајевима (на једној страни помично, на другој непомично). Према броју лежаја разликују се греда с једним лежајем (конзолна), с два лежаја (просто ослоњена, с препустима), с више лежаја (континуирана).

Опруга за коју вреди Хуков закон: сила F је сразмерна (пропорционална) растезању опруге x.

Затезно испитивање на кидалици за нестандардни испитни узорак.

Напрезање $\sigma =F/A$ углавном је просечно напрезање у пресеку. Напрезање се често не распоређује једнако у пресеку (m–m), посебно у близини места где делује спољашња сила у хватишту (n–n'').

Дијаграм напрезања (σ - затезног напрезања и ε - линијске затезне деформације) за типични нежељезни материјал:
1: Стварна граница еластичности
2: Граница пропорционалности
3: Граница еластичности
4: Граница развлачења или σ_0,2 (напрезање при којем настаје трајно продужење од 0,2% првобитне дужине шипке или штапа)

Клизачица код окретања смањује свој момент инерције скупљајући руке уз тело како би се брже окретала.

Трактор са спољашњим замашњаком (с великим моментом инерције) који служи да уједначује окретање мотора (без трзаја).

Материјал може бити оптерећен а) притисно, б) затезно, ц) смично.

Спој за топлотно истезање на мосту.

Увијање или торзија шипке (штапа) квадратног пресека.

Момент савијања узрокује нормална напрезања σ која се замишљају раздељенима по пресеку сразмерно удаљености од неутралне оси.

Слика оптерећења греде на 2 ослонца, деловање сила на греду, деловање момената савијања на греду и прогиб греде када нормална сила делује у средини греде.

Код смицања сила се примјењује на врх правоугаоника док је дно правоугаоника у месту. Настало смично напрезање, $\tau \,$, изобличује правоугаоник у паралелограм, тако да је оптерећен само врх паралелограма.

Приказ 4 Ојлерова модела извијања када настаје губитак стабилности штапа или неког другог витког елемента конструкције (на пример стуба) осно оптерећенога прекомерно великом притисном силом.

Осим назива наука о чврстоћи употребљава се и назив отпорност материјала. Оба су назива традиционална и не одговарају у потпуности. Не ради се о отпорности (чврстоћи) материјала, него о чврстоћи делова конструкција. Осим чврстоће проучава се још крутост и стабилност, па ни назив наука о чврстоћи није потпуно прикладан, иако је бољи од назива отпорност материјала. Бољи назив био би механика деформабилних чврстих тела, слично називу механика крутих тела или механика флуида. Наука о чврстоћи је у првом реду техничка (инжењерска) дисциплина којој је сврха да што једноставнијим методама на задовољавајући, приближан начин реши проблеме из техничке праксе. Понекад се сусреће и назив еластостатика, која проучава статичке проблеме еластичних тела. Ни тај назив није добра замена за назив наука о чврстоћи, јер она проучава и нееластична тела и динамичке проблеме, па се чини оправданим задржати назив наука о чврстоћи.

Историја

Већ на почетку развоја цивилизације, кад су се почеле градити веће зграде, храмови, мостови, бродови, једноставне машине и направе, било је потребно да се сакупе подаци о својствима појединих конструкцијских материјала и облика тела. Без сумње су постојала искуствена правила о одређивању мера појединих делова конструкција, јер би без њих било немогуће изградити величанствене грађевине и споменике изграђене још у старом веку. Посебно су се својим грађевинарством истицали градитељи Римског царства. Познате су њихове палате, храмови, арене, базилике, акведукти, те катапулти и друге ратне и радне машине. Нешто о методама њихова градитељства познато је из књиге De architectura libri decem од Марка Полиона Витрувија. Највећи део знања који су сакупили стари Грци и Римљани и други народи изгубљен је у току ранога средњег века.

Прве значајне експерименте о понашању и чврстоћи материјала обавио је Леонардо да Винчи на прелазу из 15. у 16. век. Он је испитивао чврстоћу жице, греда и стубова. Дошао је до исправног закључка да је чврстоћа греде на два ослонца сразмерна (пропорционална) ширини и обрнуто сразмерна распону. Није забележено да ли је испитивао утицај висине греде. Галилео Галилеј је први покушао да аналитички одреди чврстоћу појединих делова конструкција. Утврдио је да чврстоћа геометријски сличних тела опада с порастом димензија. Позната су његова разматрања о савијању штапа. Он је погрешно претпоставио да су силе (напрезање) при савијању једнолико расподељене по висини пресека греде и да се греда при лому окреће око најниже тачке ослонца. Уз ту претпоставку равнотежа момената унутрашњих и спољашњих сила око уклештеног краја правоугаоне (дужине l, ширине b и висине h) конзоле даје:

$\sigma =2\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

Тачно решење гласи:

$\sigma =6\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

Галилејево решење разликује се само за константу од тачног решења. Галилео је објавио у делу Discorsi e dimostrazioni matematische intorno a due nuove scienze attenenti alla meccanica & i movimenti locali (Лејден, 1638).

Проблем савијања греде обрађивао је и Едм Мариот. Он је у раду објављеном 1690. задржао претпоставку да неутрална линија пролази кроз доњи брид пресека, али је увео претпоставку да напрезања линеарно расту дошао је до решења:

$\sigma =3\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

То је решење ближе тачном од Галилејевог. Антван Парент (16. септембра 1666. – 26. септембра 1716) је такође разматрао савијање греде. Он је 1713. објавио два рада. У првом је показао да Мариотово решење може вредити само за правоугаони пресек и извео је израз за кружни пресек. У другом раду је пошао од претпоставке да неутрална оса пролази кроз средину пресека и дошао до исправног решења. Његов је рад, међутим, остао незапажен, па су се многи инжењери и даље служили Мариотовим решењем. Тачно решење проблема савијања греде извео је 1773. Шарл-Огистен де Кулон не познавајући Парентово решење. Он је 1784. решио проблем увијања округлог штапа и увео појам модула смицања.

Закон линеарне зависности оптерећења и помака, односно напрезања и деформације поставио је 1660. Роберт Хук на темељу експеримента с опругама. Међутим, тај закон, познат као Хуков закон, објављен је тек 1678. у књизи De potentia restitutiva, са објашњењем каква сила, такво продуљење. Томас Јанг је 1807. математички извео Хукеов закон за једноосно растезање и увео појам модула еластичности, који се по њему назива и Јангов модул еластичности. Тај је закон 1828. допунио Симеон Дени Поасон и увео појам коефицијента попречне конструкције при растезању, који се по њему назива Поасонов коефицијент или Поасонов однос.

Знатно су придонели развоју теорије еластичности и аналитичким методама о науци о чврстоћи швајцарски математичари, браћа Јакоб и Јохан Бернули. Они су разматрали деформације греде при савијању. Јакоб Бернули је увео претпоставку да при савијању попречни пресеци остају равни. Он је 1694. утврдио да је закривљеност еластичне линије пропорционална моменту савијања. Данијел Бернули, Јоханов син, први је извео диференцијалну једнакост попречних вибрација штапа. Леонард Ојлер, ученик Данијела Бернулија, такође је проучавао еластичне линије. Он је 1744. извео израз за критичну силу извијања витког штапа. Огистен Луј Коши је 1822. у раду који је предложио Француској академији наука, по први пут одредио просторно стање напрезања и извео једнакости равнотеже диференцијалног елемента. Први рад из теорије плоча објавио је Клод Луј Навје 1820. Он је такође први дао општи приступ решавању статички неодређених задатака. Теорију савијања плоча разрађивали су даље Симеон Дени Поасон, Густаф Кирхоф и други. D. Ј. Журавски је извео 1844. израз за помична напрезања при савијању греде. Емил Винклер је 1858. решио проблем савијања дебелог закривљеног штапа методама науке о чврстоћи. Тачно решење тог проблема дао је 1881. M. Головин. Увијања неких неокруглих пресека решио је 1852. Адемар Жан-Клод Баре де Сен-Венан. Године 1857. Емил Клапејрон извео је једнакост три момената (Клапејронова једнакост). Џејмс Клерк Максвел је 1870. извео теорему о реципрочности упливних коефицијената (Максвелова теорема), а Карло Алберто Казтиљијано је 1873. извео своју прву теорему. Кристијан Ото Мор је објавио рад о кружницама напрезања 1895.

Напрезање

Главни чланак: Напрезање

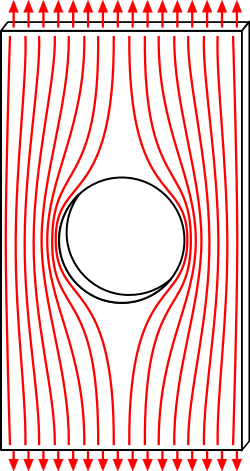
Напрезање је унутарња сила расподељена по јединици површине неког чврстог тела која се јавља као реакција на деловање спољашњих сила или промене температуре тела, с јединицом паскал (Pa = N/m²). Величина напрезања у некој тачки тела зависи од оријентације пресека тела на којем се напрезање проматра. Такво пуно напрезање је вектор генерално положен под углом према нормали на пресек и може се раставити на три скаларне компоненте везане уз координатни систем: једну у смеру нормале x на пресек (σ_x, нормално напрезање) и две на њу нормалне које леже у површини пресека у смеру преостале две осе (τ_xy и τ_xз, тангенцијална или смицаона напрезања). Узимајући сваку осу као нормалу на одговарајући пресек, произлази да у свакој тачки тела постоји девет компонената напрезања везаних уз један координатни систем, које делују на елемент запремине и које чине такозвани тензор напрезања другога реда. Због симетричности тога тензора, која следи из услова равнотеже елемента запремине, само је 6 међусобно различитих компонената, јер је τ_иј = τ_ји (на пример τ_xy = τ_yx). Како се у некој тачки мења оријентација координатних оса, тако се мењају и износи напрезања. У свакој тачки тела могућа је таква оријентација осе према којима постоје само нормална напрезања, док су помична једнака нули. Та три напрезања називају се главним напрезањима, од којих су два екстремне вредности σ_max и σ_min у тој тачки.

Због унутарњих силâ јављају се у телу деформације с којима су напрезања везана преко Хуковог закона. Чврстоћа конструктивних елемената процењује се према такозваним хипотезама или теоријама чврстоће у којима напрезања имају пресудну улогу.

Деформација

Главни чланак: Деформација

Деформација (лат. deformatio: изобличење, нагрђивање), у физици, је промена облика тела (растезање, савијање, усукивање и друго) под утицајем спољашњих или унутарњих сила. Може бити еластична, када се након престанка деловања силе тело враћа у првобитни облик, и нееластична, када деформисани облик остаје и након престанка деловања силе.

Дијаграм напрезања

Главни чланак: Дијаграм напрезања

Дијаграм напрезања приказује медусобну зависност σ - затезног напрезања и ε - релативног продужења или линијске затезне деформације. У материјалу који је оптерећен неком силом F настају напрезања σ која узрокују његово растезање. Напрезање σ је однос силе F и површине А пресека штапа или шипке (нормалног на однос силе).

$\sigma ={\frac {F}{A}}$

Због деловања силе F (а тиме насталог напрезања σ) штап или шипка ће се од почетне дужине L₀ растегнути на дуљину L. Тако је продужење штапа или шипке:

$\varepsilon ={\frac {\Delta L}{L_{0}}}={\frac {L-L_{0}}{L_{0}}}$

Релативно продуљење ε (дуљинска или уздужна деформација) штапа или шипке је продужење с обзиром на почетну дужину L_o. Почетно је напрезање линеарно (деформација је директно сразмерна напрезању). У подручју линеарног растезања (Хуков закон) материјал је еластичан и након престанка деловања силе, односно напрезања, он се враћа у почетно стање. Јангов модул еластичности је однос напрезања и релативног продужења (у подручју еластичности).

Техничка граница еластичности је напрезање при којем осетљиви инструменти осете прво приметно трајно продужење материјала (при још непромењеном пресеку А_о). Након те границе (обично на крају линеарног растезања) материјал се растеже пластично и након престанка деловања силе не враћа се више на почетну дужину L₀, већ остаје одређено трајно продужење, уз сужење пресека, А < А₀).

Геометријска својства пресека

Момент инерције

Главни чланак: Момент инерције

Момент тромости или момент инерције (знак I или J) је физичка величина која описује тромост или инерцију честице или крутог тела при промени брзине или смера вртње; једнака је збиру умножака масе m и квадрата удаљености r од осе ротације сваке честице која чини тело:

$I=\sum _{i=1}^{N}m_{i}{r_{i}}^{2}$

Момент инерције неког тела зависи од облика тела, расподеле масе, положаја осе ротације. На пример, ако је m маса тела, r његов полупречник, а оса ротације уједно и оса симетрије, момент инерције на пример шупљег ваљка или прстена износи:

$I=mr^{2}$

хомогено испуњеног ваљка или кружне плоче:

$I={\frac {mr^{2}}{2}}\,\!$

хомогено испуњене кугле:

$I={\frac {2mr^{2}}{5}}\,\!$

Момент инерције хомогено испуњеног штапа којему је оса ротације нормална на дужину штапа налази се на половини дужине штапа:

$I={\frac {mr^{2}}{12}}\,\!$

а на крају је штапа:

$I={\frac {mr^{2}}{12}}\,\!$

где је: r - дужина штапа. Мерна је јединица момента инерције килограм пута квадратни метар (kg m²).

Напрезање и деформирање штапа

На штапу као моделу тела којем је једна мера или димензија (дужина) знатно већа од друге две постоје једноставна оптерећења: растезање, увијање, савијање, извијање и друга.

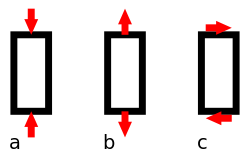
Истезање и притискање

Штап је осно или аксијално оптерећен ако су у сваком пресеку штапа све компоненте осим нормалне силе (уздуж осе штапа) једнаке нули. У средишњем су делу напрезања једнолико расподељена и у њима напрезање износи:

$\sigma ={\frac {F}{A}}$

где је: F - нормална сила на штап, а А - површина попречног пресека штапа. Ако је дужина штапа много већа од дебљине (l / h > 10 - 20), може се утицај одступања од једноликог напрезања у рубном прелазном подручју на продужење занемарити. Тада је:

$\Delta l=\varepsilon \cdot L$

где је: Δ l - промена дужине, а l - дужина штапа. Применом Хуковог закона израз прелази у:

$\Delta l={\frac {F}{E\cdot A}}\cdot l={\frac {\sigma }{E}}\cdot l$

где је: Е - Јангов модул еластичности.

Топлотна напрезања

Топлотна напрезања σ_T појављују се при загреавању или хлађењу чврсто фиксираних предмета:

$\sigma _{T}=E\cdot \varepsilon =E\cdot {\frac {\Delta l}{l}}$

где је: Δ l - дужинско или линеарно топлотно истезање (или скраћење):

$\Delta l=\alpha _{L}\cdot l_{0}\cdot \Delta T$

где је: l₀ - почетна дужина, ΔT - температурна разлика, α_L - коефицијент топлотног истезања. Топлотна напрезања упетог штапа произлазе:

$\sigma _{T}=E\cdot \alpha _{L}\cdot \Delta T$

Топлотна напрезања не зависе од размера предмета и могу бити каткада врло велика.

Увијање или торзија

Главни чланак: Торзија

Увијање или торзија (каснолат. torsio: увртање, увијање) је начин оптерећења елемента конструкције када око неке његове осе делују два једнака и супротно усмерена момента (спрега). Тако су на пример оптерећена вратила радних машина или погонске осовине возила када на њих са једне стране делује погонски момент, а са друге отпор радног дела машине (на пример алата) или точка возила. Слично могу бити оптерећени и стубови носећих металних конструкција (дизалица, грађевина, далековода и слично), који су једним крајем уклештени у темеље, а на другом стално или само повремено (удари ветра) делује момент који стуб увија око његове уздужне оси. Елементи оптерећени на увијање поједноставњено се приказују штаповима, а прорачунима им се одређују деформације (угао увијања) и напрезања (смицање, ређе и нормална). За равне штапове попречног кружног пресека или пресека у облику кружног венца (на пример шупље осовине) прорачуни се са високом тачношћу спроводе уз претпоставке да при увијању попречни пресеци остају равни и нормални на уздужну осу штапа, да се пресеци закрећу као круте фигуре (полупречници при закретању остају равни) те да се на пресецима не јављају нормална напрезања. У средишту пресека таквог штапа помично напрезање једнако је нули, а на вањском рубу пресека, полупречника r, оно има максималну вредност:

$\tau ={\frac {M_{t}\cdot r}{I_{p}}}$

где је: M_t - момент торзије или увијања, а I_p поларни момент инерције површине пресека у односу на средиште, који за пуни пресек износи:

$I_{p}={\frac {\pi \cdot r^{4}}{2}}$

а за кружни венац, унутарњег и спољашњег полупресека r и R:

$I_{p}={\frac {\pi \cdot (R^{4}-r^{4})}{2}}$

Код тога ће се крајњи пресеци штапа дужине l и модула смицања G, који зависи само од врсте материјала штапа, закренути један у односу на другог за угао

$\phi _{}={M_{t}\cdot l \over I_{p}\cdot G}$

Код увијања неокруглих штапова попречни се пресеци искривљују, наведене претпоставке више не вреде, а прорачуни помичних напрезања и деформација су сложенији. У границама Хуковог закона момент торзије M_t и угао закрета φ међусобно су пропорционални, тако да вреди:

$M_{t}=D\cdot \phi$

D је такозвани дирекцијски момент (торзијска крутост) са јединицом Nm/rad, који за штап пуног кружног пресека или кружнога венца износи G Ip / l.

Савијање

Главни чланак: Савијање

За разлику од осног оптерећења (истезање и притисак), при савијању штапа деформише се уздужна оса штапа. Деформисана уздужна оса зове се еластична линија или прогиб. Разликује се чисто савијање и попречно савијање. При чистом савијању све су компоненте унутрашњих сила једнаке нули, осим момента савијања. При попречном савијању осим момента савијања појављује се још и попречна сила која узрокује смицање. Чисто савијање зове се још и савијање спреговима, а попречно савијање, савијање силама. Момент савијања узрокује нормална напрезања σ која се замишљају раздељенима по пресеку сразмерно удаљености од неутралне осе. Неутрална оса пролази кроз тежиште проматраног пресека. Класична једнакост која одређује напрезање у греди услед деловања чистог савијања је:

${\sigma }={\frac {M\cdot y}{I_{x}}}$

где је: ${\sigma }$ - напрезање услед савијања, M - момент савијања око неутралне осе x, y - нормална удаљеност од неутралне осе x, I_x - моменат инерције или моменат тромости око неутралне осе x.

Максимално напрезање на савијање σ_max појављује се у тачки која је најудаљенија од неутралне осе y_max:

$\sigma _{max}={\frac {M\cdot y_{max}}{I_{x}}}={\frac {M}{W_{x}}}$

где је: ${W_{x}}$ - момент отпора пресека.

Прогиб носача ${\delta }$ произлази из диференцијалне једнакости еластичне линије:

${\delta }={\frac {M_{x}}{E\cdot I_{x}}}$

Уобичајене вредности за максималне моменте савијања, прогибе, моменте тромости и моменте отпора пресека дате су у таблицама.

Смицање

Главни чланак: Смицање

Смицање, смик, посмик или одрез је оптерећење чврстог тела силама које делују у равни неког пресека тела, а настоје да изазову паралелно клизање једног дела пресека (танкога слоја) у односу на други. Тако су на пример оптерећене заковице које спајају крајеве металне траке у обруч, када дуж обруча делују затезне силе. Једнако тако, код торзије (увијања) штапа округлог пресека моментима (на пример вратило), пресеци нормални на уздужну осу штапа напрегнути су на смицање. Смично оптерећење користи се у неким технолошким поступцима, као што је на пример резање маказама, пробијање штанцањем и друго. У елементима конструкција смицање се најчешће јавља заједно са савијањем. Последица су смицања реактивна смицаона (тангенцијална) напрезања τ која леже у равни пресека тела, а расподељена су по неком закону зависно од начина деловања сила и момената. Тако су код савијања штапова силама напрезања расподељена параболично, код увијања линеарно и тако даље. У општем случају оптерећења, на сваки бесконачно мали елемент површине делују, осим нормалних, и смицаона напрезања, која чине спрегове. Под деловањем тих спрегова долази до промене првотно правог угла између две међусобно нормалне странице елемента за мали угао γ (угаона деформација), који мерен у радијанима код еластичних деформација износи:

$\gamma ={\tau \over G},$

где је: G - модул смицања завистан од материјала (спрега сила).

Извијање

Главни чланак: Извијање

Извијање је губитак стабилности штапа или неког другог витког елемента конструкције осно оптерећеног прекомерно великом притисно силом. Тако се на пример штап, постављен нормално на тло и одозго притиснут притисном силом, извије (избочи) у тренутку када се сила повећа преко одређене границе (Ојлерова критична сила). Решеткасте конструкције које су састављене од штапова (стубови далековода, челични мостови, дизалице) обично губе стабилност због извијања једног или више штапова, па се у прорачунима таквих конструкција посебна пажња посвећује притисно најоптерећенијим штаповима. Интензитет критичне силе при којем настаје извијање зависи од виткости штапа, то јест начина учвршћења његових крајева и његовим геометријским својствима, те о механичким својствима материјала од којег је штап начињен. Код конструкција са плочама и љускастим елементима извијање је сложеније. Критичном силом бавио се швајцарски математичар, физичар и астроном Леонард Ојлер, по којем је та сила и названа.

Литература

• Фа-Хwа Цхенг, Инитиалс. (1997). Стренгтх оф материал. Охио: МцГраw-Хилл
• Мецханицс оф Материалс, Е.Ј. Хеарн
• Алфиревић, Иво. Стренгтх оф Материалс I. Техничка књига. 1995. ISBN 978-953-172-010-6..
• Алфиревић, Иво. Стренгтх оф Материалс II. Техничка књига. 1999. ISBN 978-953-6168-85-9..
• Ashby, M.F. Materials Selection in Design. Pergamon, 1992.
• Beer, F.P., E.R. Johnston, et al. Mechanics of Materials, McGraw-Hill. (3rd изд.). 2001. ISBN 978-0-07-248673-5. 
• Цоттрелл, А.Х. Мецханицал Пропертиес оф Маттер. Wилеy, Неw Yорк, 1964.
• Ден Хартог, Јацоб П. Стренгтх оф Материалс. Довер Публицатионс, Инц. 1961. ISBN 978-0-486-60755-9..
• Drucker, D.C. Introduction to Mechanics of Deformable Solids. McGraw-Hill, 1967.
• Gordon, J.E. The New Science of Strong Materials. Princeton, 1984.
• Groover, Mikell P. Fundamentals of Modern Manufacturing, John Wiley & Sons,Inc. (2nd изд.). 2002. ISBN 978-0-471-40051-6. .
• Хасхеми, Јавад анд Wиллиам Ф. Смитх. Фоундатионс оф Материалс Сциенце анд Енгинееринг, МцГраw-Хилл. (4th изд.). 2006. ISBN 978-0-07-125690-2. .
• Хиббелер, Р.C. Статицс анд Мецханицс оф Материалс, СИ Едитион. Прентице-Халл. 2004. ISBN 978-0-13-129011-2..
• Лебедев, Леонид П. анд Мицхаел Ј. Цлоуд. Аппроxиматинг Перфецтион: А Матхематициан'с Јоурнеy инто тхе Wорлд оф Мецханицс. Принцетон Университy Пресс. 2004. ISBN 978-0-691-11726-3..
• Gent, A.N.; Mars, W.V. (2013). „Strength of Elastomers”. Ур.: James E. Mark; Burak Erman; Mike Roland. The Science and Technology of Rubber (4th изд.). стр. 473—516. ISBN 9780123945846. doi:10.1016/B978-0-12-394584-6.00010-8. 
• Mott, Robert L. Applied Strength of Materials, Prentice-Hall. (4th изд.). 2002. ISBN 978-0-13-088578-4. .
• Попов, Егор П. Енгинееринг Мецханицс оф Солидс. Прентице Халл, Енглеwоод Цлиффс, Н. Ј. 1990. ISBN 978-0-13-279258-5..
• Рамамрутхам, С. Стренгтх оф Материалс.
• Схамес, I.Х. анд Ф.А. Цоззарелли. Еластиц анд инеластиц стресс аналyсис. Прентице-Халл. 1991. ISBN 978-1-56032-686-1..
• Timoshenko S. Strength of Materials, Krieger Publishing Company. (3rd изд.). 1976. ISBN 978-0-88275-420-8. .
• Тимосхенко, С.П. анд D.Х. Yоунг. Елементс оф Стренгтх оф Материалс, 5тх едитион. (МКС Сyстем)
• Давидге, Р.W., Мецханицал Бехавиор оф Церамицс, Цамбридге Солид Стате Сциенце Сериес, (1979)
• Лаwн, Б.Р., Фрацтуре оф Бриттле Солидс, Цамбридге Солид Стате Сциенце Сериес, 2нд Едн. (1993)
• Греен, D., Ан Интродуцтион то тхе Мецханицал Пропертиес оф Церамицс, Цамбридге Солид Стате Сциенце Сериес, Едс. Цларке, D.Р., Суресх, С., Wард, I.M.Бабу Том.К (1998)

Спољашње везе

• Фаилуре тхеориес
• Цасе студиес ин струцтурал фаилуре